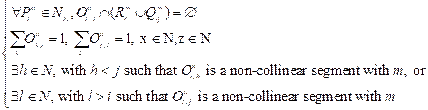Article
citation information:
Nguyen,
N.H.Q., Nguyen, N.Q.N., Nechaev, V.N. Optimizing alternative air traffic service
routes for airport disruption contingency management. Scientific Journal of Silesian University of Technology. Series
Transport. 2025, 129, 169-190. ISSN:
0209-3324. DOI: https://doi.org/10.20858/sjsutst.2025.129.10
Ngoc Hoang Quan NGUYEN[1],
Ngoc Quynh Nhu NGUYEN[2],
Vladimir Nikolaevich NECHAEV[3]
OPTIMIZING
ALTERNATIVE AIR TRAFFIC SERVICE ROUTES FOR AIRPORT DISRUPTION CONTINGENCY
MANAGEMENT
Summary. Flight disruptions due
to destination airport unavailability present significant challenges for air
traffic management and airline operations. These situations may lead to
cascading delays, increased fuel consumption, and reduced passenger
satisfaction. A key response strategy is the timely identification of
alternative air traffic services (ATS) routes to suitable diversion airports
while ensuring flight safety and operational continuity. However, existing
diversion approaches often rely on static contingency plans or real-time
decisions by air traffic controllers, which may not perform well under dynamic
conditions. To address this, a robust multi-objective optimization model based
on the A-star algorithm is proposed to dynamically identify optimal alternative
air traffic services routes when the planned destination becomes inaccessible.
The model accounts for multiple objectives, including route efficiency, safety,
and operational feasibility, across pre-tactical and tactical phases of air
traffic flow management. By integrating airspace constraints and traffic flow
considerations, the model supports adaptive, data-informed decision-making.
Simulation results demonstrate the model’s ability to reduce network
disruptions and support safe, efficient diversions under various traffic
scenarios. This study contributes to enhancing the resilience of the air
transportation system and provides a foundation for future integration into
intelligent air traffic management tools and decision support systems.
Keywords: alternative ATS route, air traffic management, destination airport
unavailable, A* algorithm, multi-objective optimization model
1.
INTRODUCTION
Air transportation is a cornerstone of global
connectivity, but it is inherently vulnerable to disruptions caused by adverse
weather, technical malfunctions, security threats, and other unforeseeable
events. In the event of airport inoperability, aircraft must be promptly
reassigned to alternative destinations through optimized ATS routing to ensure
safety, reduce economic impact, and sustain operational continuity
Recent statistical data underscores the
significance of this issue. According to the U.S. Bureau of Transportation
Statistics (BTS, 2025), a total of 15,059 flights operated by the ten major
airlines were diverted to alternate airports in 2024 alone, compared to 14,864
in 2023. Similarly, data from Eurocontrol (2024) reveals that in 2022, out of
9.3 million flights within the EUROCONTROL Network Manager area, 28,738 flights
(0.3%) landed at an airport different from their originally intended
destination, and the estimated cost per diverted flight was approximately
€8,800. In addition to direct operational costs, unplanned diversions impose
significant financial burdens on airlines, airports, and passengers. According
to the Federal Aviation Administration (FAA, 2020), the variable operating cost
per flight hour is $1,508, while the average cost of a flight cancellation per
passenger is approximately $15.51. These figures, when multiplied across
thousands of diverted flights annually, represent substantial economic losses
for the aviation industry. Beyond monetary considerations, flight diversions
also contribute to logistical challenges, including increased air traffic
congestion, additional fuel consumption, crew scheduling complexities, and
passenger inconvenience. Moreover, flight diversions cause ripple effects
beyond immediate disruptions. They can delay connecting flights, burden ATC and
alternate airports, and strain limited resources. Prolonged ground delays and
passenger reallocation may also damage airline reputation and customer loyalty,
with lasting impacts on passenger behavior.
Although diverted flights account for a small
portion of total operations, their cumulative impact on ATM efficiency and
safety is significant. This underscores the need for advanced strategies to
identify alternative ATS routes, supported by real-time adaptive ATM systems
and predictive analytics. Emerging approaches increasingly rely on optimization
models powered by AI and advanced algorithms, enabling real-time disruption
prediction and route optimization. However, despite their promise, the application
of such innovations to the dynamic selection of alternative ATS routes remains
an underexplored area. Most existing studies tend to address peripheral topics
rather than directly confronting this critical challenge.
Several notable studies have explored
optimization techniques relevant to trajectory adjustments. Xu et al. (2020)
proposed a collaborative ATFM framework utilizing Mixed-Integer Linear
Programming to optimize cost-efficient trajectory adjustments and minimize
delays for airspace users. Similarly, Yang et al. (2021) introduced a robust
optimization model designed to enhance adaptability and efficiency in
identifying alternative ATS routes for flights under uncertain adverse weather
conditions. Another study focused on a robust optimization framework for flight
diversions under uncertainty, balancing stakeholder interests with operational
performance (Bongo and Sy, 2020). However, the aforementioned studies primarily
focus on optimizing real-time or pre-tactical trajectory adjustments for
aircraft, rather than developing a comprehensive optimization framework capable
of determining alternative routes when the original ATS route becomes
unavailable. More notably, there is a near absence of research dedicated to
identifying alternative routes when the original destination airport (or
transfer of control point) is rendered unusable. This gap highlights a
promising research direction focused on developing an advanced optimization
model that can dynamically identify alternative ATS routes across different
phases of ATFM (pre-tactical, or tactical), while satisfying specific
operational constraints and performance objectives.
In light of these challenges, it is essential to
develop an optimized decision-support framework for identifying alternative ATS
routes when the planned destination airport becomes unavailable. This study
proposes a robust model based on the A* algorithm to determine the most
efficient route to an alternate airport under two cases. The first involves the
unavailability of the destination airport alone – due to technical issues or
on-ground incidents – while the second addresses broader disruptions, including
surrounding airspace and portions of the original route (hereafter referred to
as the No-fly Area), as seen in adverse weather or airspace restrictions. These
cases present varying levels of complexity, particularly in maintaining
regulatory compliance and safety. In both cases, the model aims to minimize
total flight distance to ensure operational efficiency and feasibility.
To address the added complexity of the second
case, three routing scenarios with additional sub-objectives are introduced:
(1) minimizing deviation from the original route, (2) minimizing the total
distance from the original start to the new destination, and (3) enabling
user-defined preferences for flexible routing. These scenarios enhance the
model’s practical applicability across different ATFM phases. Scenarios 1 and 2
are best suited for pre-tactical planning, where minimizing flight time
(Scenario 2) or maintaining route consistency (Scenario 1) supports efficiency
and conflict avoidance. Scenario 3, offering flexible user input, is more
appropriate for the tactical phase, which requires real-time responsiveness to
actual traffic and airspace conditions.
To evaluate the efficiency and responsiveness of
the proposed model in dynamically identifying alternative ATS routes, the ATS
route network within the HCM FIR has been selected as the primary case study.
The HCM FIR holds a strategically significant geographical position (Carreras
and Greenman, 2017; Nguyen Le Quyen, 2022), serving as a critical aviation hub
that connects countries in the Northern Hemisphere – particularly Russia and
China – to those in the Southern Hemisphere, including Oceania. Additionally,
it borders the vast South China Sea, a region that accommodates multiple
crucial international ATS routes. In addition to its strategic location,
Vietnam has one of the fastest-growing aviation industries in the world
(International Trade Administration, 2024; 6Wresearch, 2022). The country’s air
transport sector has experienced significant expansion in recent years, driven
by increasing passenger demand, economic growth, and enhanced connectivity with
global markets. The HCM FIR plays an essential role in facilitating this
growth, serving as a critical gateway for both domestic and international air
traffic. Another key factor that underscores its significance is the relatively
high air traffic density on several routes within the FIR. For instance, the
HCM – Hanoi route, which largely falls within this FIR, ranks as the fourth
busiest domestic air route in the world (OAG, 2024). Furthermore, the weather
conditions in this region can be highly complex at times due to the influence
of monsoons and tropical storms originating from the South China Sea. These
adverse weather patterns frequently disrupt flight schedules, requiring not
only frequent ATS route reconfigurations but also necessitating aircraft
diversions to alternate airports. A notable example occurred on May 16,
2023, when seven flights originally scheduled to land at Tan Son Nhat
International Airport were unable to do so and had to divert to alternate
airports due to unfavorable weather conditions (Vietnamplus, 2023). Given these factors, selecting the HCM
FIR as a case study is highly appropriate, as it ensures both practical
relevance and a robust scientific foundation. Moreover, the insights gained
from this analysis can enhance the potential for broader implementation in
other high-density airspaces worldwide, particularly in regions where adverse
weather conditions frequently necessitate the identification of alternative ATS
routes and airport diversions.
2.
METHODOLOGY FOR OPTIMIZING ALTERNATIVE ATS ROUTES DURING AIRPORT DIVERSIONS
2.1. A*
algorithm
The
A* algorithm is one of the most widely used and efficient pathfinding
algorithms in computer science and artificial intelligence. It is a heuristic
search algorithm that extends Dijkstra’s Algorithm by incorporating heuristic
information to improve efficiency (Beeker, 2004). The fundamental principle of
A* is to find the shortest route between a start node and a goal node in a
weighted graph while balancing exploration and optimality. A* operates using a cost function:
where:
g(n)
represents the actual cost from the start node to node n,
h(n) is
the heuristic estimate of the cost from 𝑛 to
the goal,
f(n) is
the estimated total cost of the path through node 𝑛.
The
choice of heuristic function significantly influences the performance of A*,
with an admissible (never overestimates the true cost) and consistent (follows
the triangle inequality) heuristic ensuring both optimality and efficiency.
Compared to uninformed search methods, A* intelligently prioritizes promising
paths, reducing unnecessary exploration and enhancing computational speed. It
guarantees an optimal solution if the heuristic function does not overestimate
the actual cost. This characteristic makes A* particularly effective in solving
shortest route problems in large-scale environments. The algorithm’s ability to
balance accuracy and efficiency has made it a fundamental tool in artificial
intelligence and operations research. Its scalability and robustness ensure its
continued relevance in modern computational problem-solving, making it one of
the most powerful techniques for optimal pathfinding in complex systems,
including transportation networks (Felix et al, 2024; Wang et al., 2024),
robotic navigation (Ju et al, 2020; Kabir et al, 2024), and game environments
(Kurniawan et al, 2024), where real-time decision-making and adaptability are
crucial for efficiency and performance.
In
the field of aviation in general and ATM in particular, the A* algorithm has
been widely applied to determine optimal flight routes for both manned civil
aircraft (Ma et al. 2022; Neretin et al. 2021; Li et
al. 2023; Roy, 2023) and unmanned aerial vehicles (Mandloi
et al. 2021; Ji et al. 2024). However, most existing studies focus on initial
trajectory planning rather than the dynamic re-routing of ATS paths under
operational constraints. This research addresses that gap by proposing a
re-routing model capable of optimizing alternative ATS routes while ensuring
efficiency and regulatory compliance. Designed for use across pre-tactical and
tactical phases, the model adapts to diverse scenarios and disruptions,
enhancing the flexibility and resilience of ATS route planning in complex
airspace environments.
2.2. Steps for
Developing Optimization Models and Mathematical Models
Since the A-Star (A*) algorithm
is a branch of graph theory, the airspace structure in this study is
represented as a graph G = (N,O) where 
, and 
. In this representation, N
consists of waypoints and airport coordinates (collectively referred to as
nodes), while 𝑂 represents the arcs, each
defined as a direct connection between two nodes. Each arc 𝑂 is characterized by two key
parameters: distance (𝑑) and angle (𝜃).
A crucial aspect of data
preprocessing is ensuring the accurate input of node coordinates, as precise
spatial representation is fundamental for effective route optimization. To
achieve this, the latest aeronautical data from the Vietnam AIP 2024 is utilized,
incorporating a total of 130 nodes into the airspace model. Figure 1
illustrates the spatial relationships among these nodes, providing a graphical
representation of the airspace network structure.
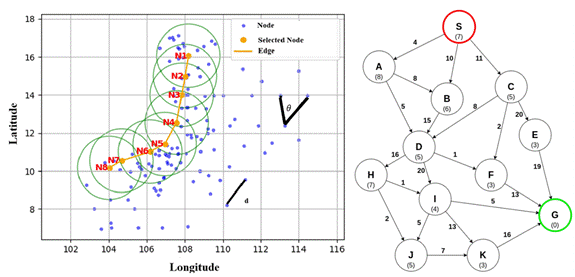
Fig. 1. Illustrating the Structure of Airspace
in the Model
and Establishing Relationships Between Nodes
After
completing the airspace structure description using nodes, the next step is to
establish relationships between them, specifically defining parent-child
connections. This hierarchical relationship is essential for optimizing route
search processes. Given that the HCM FIR encompasses both land and sea areas,
the airspace structure is systematically divided into two distinct regions:
land–coast and coast-sea. To determine how nodes are connected, a systematic
selection process is applied. Each node identifies neighboring
nodes within a specified radius, forming a structured network. The node at the center of this defined area is designated as the parent
node, while all surrounding nodes that fall within the radius are considered
child nodes. A directional scanning technique is used, where the search is
conducted in one-degree increments. In each direction, at most one child node
is selected, ensuring an even distribution of connections and preventing
unnecessary redundancy. This method enhances the efficiency of route
calculations and ensures a well-structured node hierarchy for optimal airspace
navigation. Figures 2 and 3 illustrate all node connections in the land – coast
and coast – sea regions, respectively. Land nodes are shown in green, sea nodes
in blue, and coastal nodes – appearing in both figures – are marked in pink.
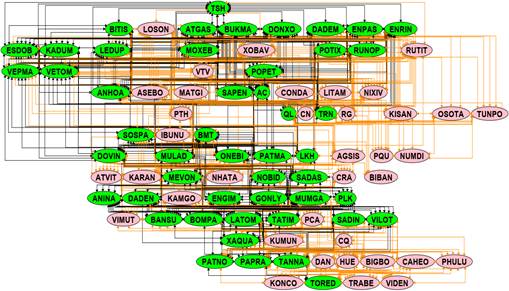
Fig. 2. Connections between all nodes in the
land-coast region
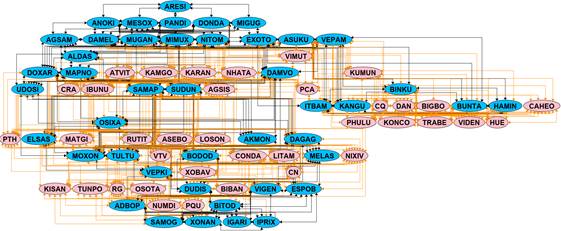
Fig. 3.
Connections between all nodes in the coast-sea region
The
next crucial step in the model development is the precise definition of the
objective function, constraints, and assumptions that will be applied within
the model. This phase is fundamental, as it forms the conceptual and
mathematical backbone of the model, ensuring its effectiveness, feasibility,
and real-world applicability. Without a well-defined structure, even the most
sophisticated models may fail to produce meaningful or actionable insights. In
this model, the primary objective, across all scenarios and cases, is to
minimize the distance of the alternative route to the newly designated airport,
as specified by the user. This objective is particularly important in urban
planning, logistics, and transportation network optimization, where shorter travel
distances directly translate to lower operational costs, reduced travel time,
and improved user satisfaction. The objective function
is defined mathematically as:
where:
d is
the distance between any two consecutive nodes i
and i+1 on the ATS route that consists of u nodes.
D is
the total distance from the starting node to the ending node.
For
each ATS route, the following variables are defined:
·
: A
node positioned along ATS route a between the start and end node,
defined by its latitude and longitude. Note: 
,
indicating that for each ATS route a, the node 
ranges from 0 to 
. Specifically:
When 
,
it corresponds to the starting node of ATS route 
and must coincide with the starting point of
the original route.
When 
,
it corresponds to the ending node of ATS route and must not coincide with the ending point of
the original ATS route. In other words, n represents the newly selected
destination airport.
·
):
Indicates the latitude and longitude of the node .
·
:
The length of the arc connecting node to node 
along ATS route .
This value is calculated using the following formula.
·
:
The arc to 
on ATS route .
The variable is defined as a binary variable, specifically:
Some
special variables related to the original ATS route t are listed as follows:
·
:
represents the starting node on the ATS route t.
·
:
represents the node at position i on the ATS route t.
·
:
represents the ending node on the ATS route t that cannot be used.
·
:
The area q of a polygonal area containing the original destination
airport of route t within the structured airspace 
,
where aircraft operations are limited.
·
: A
circle with radius r centered at a designated
point, contains the original destination airport of route t within the
structured airspace ,
where aircraft operations are limited.
In
this study, when the initial ATS route t encounters a No_fly_area
in the form of a circular with radius or a polygonal area ,
an alternative ATS route a must be identified to avoid these limited area and
reach a newly designated airport specified by the user (when at least one
No_fly_area contains the original destination airport). In cases where only the
node 
representing
the destination airport is limited, the aircraft will be unable to use this
location.
·
Node: ∀ 
∈ N,
( 
, 
) 
O: In a blocked state, cannot establish any arcs to any other node,
where v is any node belonging to N. In this case:
-
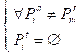
Circular area:
-
Polygon area:
In Case 1 and
Scenario 2 of Case 2, when determining an alternative route for the original
route due to a change in the destination airport, and this airport is limited
either as a single point, within a polygonal region, or within a circular area,
compliance with Equation (2) and one of the Equations (5), (6), or (7),
corresponding to the shape of the No_fly_area, must
be ensured. Additionally,
the following equation must also be satisfied.
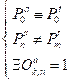
For Scenario 1
in Case 2, in addition to satisfying Equation (2) and one of the three
Equations (5), (6), or (7) depending on the shape of the No_fly_area,
an additional objective function will be formulated. This function aims to
ensure that the alternative route changes as little as possible from the
original route while still avoiding all No_fly_area
that the original route intersected, including at least one area containing the
original destination airport.
In Scenario 3,
to ensure flexibility, users are given the option to reutilize nodes from the
original route t, excluding those located within any designated No_fly_area, to construct an alternative route a. An
additional objective function will be built:
In equations
(9) and (10), i represents the last available
node before all No_fly_area, and j represents
the first available node after all No_fly_area along
the route t.
Once the
objective functions are established, the model's fundamental constraints will
be identified and mathematically expressed as equations.
Constraint 1:
An ATS route a must establish a continuous path between the start node
and the end node, ensuring that no arcs lead into the start node or originate
from the end node. This constraint is mathematically represented by two equations.
Constraint 2:
For each intermediate node i (excluding the
start and end nodes), the number of incoming arcs must equal the number of
outgoing arcs. This flow balance condition
is represented by Equation (13).
To ensure that
the model can function effectively across all phases of ATFM while maintaining
both operational feasibility and alignment with real-world conditions, a set of
well-defined assumptions is established. These assumptions aim to balance the
model’s practical applicability with its optimization objectives, ensuring that
real-world constraints are incorporated without significantly compromising
computational efficiency or solution quality. By defining these operational
conditions in advance, the model can better accommodate the complexities of ATM
while maintaining robustness and adaptability to dynamic cases:
- Navigation Infrastructure: All navigation systems,
including Non-Directional Beacons, VHF Omnidirectional Range, and Global
Navigation Satellite Systems, are assumed to function reliably, providing
continuous and consistent coverage within designated areas. In the event of
system failures, relevant notifications will be issued, and affected nodes will
be removed from the input graph to maintain model integrity.
- Airspace Organization and Utilization: The structure
and boundaries of controlled airspace are considered static and unchanging
throughout the operational period. During pre-tactical phases, any
establishment of a No_fly_area due to military
operations or other restricted activities will be communicated in advance to
ATFM units to facilitate appropriate planning and adjustments.
- Meteorological Conditions: Adverse weather phenomena
are assumed to be forecasted accurately, allowing them to be represented as
polygons or circular areas defined by precise coordinates for integration into
the model. This ensures that weather constraints are effectively incorporated
into operational planning.
- Aircraft Operations: All aircraft are assumed to
operate under standard protocols without disruptions or priority handling due
to emergencies or unforeseen contingencies.
- The model assumes that all nodes are accessible for
the selection of alternative ATS routes, except those explicitly restricted by
predefined constraints. The connections between these nodes are established
based on geographic proximity and operational viability, ensuring that all
generated routes conform to existing airspace structures.
To ensure the
flexibility, dynamism, and adaptability of the model, No_fly_area
will be dynamically defined by inputting coordinate data based on notifications
received either during the planning phase or in real-time. Once these zones are
established, the model will identify valid nodes and permissible connections to
be incorporated into the optimization framework. This approach guarantees that
alternative routes are continuously updated in alignment with real-world
conditions while adhering to the existing airspace structure. Additionally, by
continuously adapting to evolving constraints, the system not only optimizes
operational efficiency but also upholds strict compliance with safety and
regulatory frameworks.
The
model's dynamic approach allows for the continuous optimization of alternative
routes, taking into account real-time airspace conditions, regulatory
constraints, and overall operational efficiency. By doing so, it ensures that
the designated alternative route is not only precise but also practical and
adaptable to evolving scenarios. This capability enhances the effectiveness of
ATM and route planning by minimizing disruptions, improving flight safety,
enhancing route reliability, and ensuring seamless integration with existing
airspace structures, ultimately contributing to a more resilient and efficient
aviation system. The final step of the model is to determine the heuristic
function used. In the A-star algorithm, selecting an appropriate heuristic
function is crucial, as it significantly impacts the optimization performance
of the model. This has been well-documented in previous research (Foead et al., 2025; Sathvik & Patil, 2021). The authors
conducted a comprehensive evaluation, and the results indicate that both the
Euclidean and Gaussian heuristic functions yield optimal outcomes (Nguyen et
al., 2025). However, the Euclidean function is simpler to implement. Therefore,
in this model, the Euclidean heuristic function will be adopted to enhance computational
efficiency while maintaining optimal performance.
3. RESULTS AND
DISCUSSION
To
run the model effectively, the first essential step is to identify the No_fly_area. A thorough assessment of airspace usage,
particularly for military operations, was conducted, and reports from the Civil
Aviation Authority of Vietnam regarding airports that frequently experience
flight diversions were reviewed. Based on these analyses, several
representative No_fly_areas were identified for
implementation in the model, and the results are presented in this study.
Regarding meteorological conditions, the complexity and variability of weather
patterns make it challenging to predefine specific areas for case studies
within the model. However, this limitation can be easily addressed in practical
applications, as the model is designed to automatically integrate the No_fly_area data by allowing real-time data input. As a
result, when deployed in real-world scenarios, the identification of restricted
areas due to adverse weather conditions becomes a seamless and efficient
process.
First,
the results for Case 1 are presented, in which the originally designated
arrival airport is unavailable for operations, while the surrounding airspace
remains functional. In this scenario, it is assumed that Phu Quoc International
Airport (PQU) must temporarily close due to technical equipment failure or an
aircraft incident. Consequently, Can Tho International Airport (TRN) is
designated as the alternate airport. The following two results will be
presented: The first result examines the situation where only PQU is
unavailable, affecting the establishment of ATS routes. The second result
extends the analysis by considering an additional operational issue. It assumes
that, in addition to PQU, the waypoints TATIM, and DONXO also become unusable
due to further constraints. Figure 4 illustrates the model's results regarding
the impact on initial routes across the entire ATS network due to operational
disruptions at PQU, as well as the process of inputting data for the newly
designated destination airport (referred to as new_end_node
in our model). Table 1 presents the route analysis results, including a list of
waypoints and the length of each route in the outcomes of Case 1. The analysis
indicates that two affected routes must be redirected via alternative ATS
routes to TRN. Figure 5 presents the results when only PQU is unavailable,
while Figure 6 depicts the case where PQU, TATIM, and DONXO are all
inaccessible.
Fig. 4. The route analysis results are
affected by Case 1
Tab. 1
The detailed results of the routes
include a list of waypoints and lengths in Case 1
|
|
Original route |
Alternative route
Case 1, Result 1 |
Alternative route
Case 1, Result 2 |
|
CRA – PQU |
602.243 km CRA - SOSPA - LKH - KADUM - SAPEN -
KISAN - PQU |
644.77 km CRA - SOSPA - LKH - KADUM - SAPEN -
KISAN - TRN |
644.77 km CRA - SOSPA - LKH - KADUM - SAPEN -
KISAN - TRN |
|
DAN – PQU |
885.749 km DAN - TATIM
- DADEN - MULAD - DONXO - POPET - KISAN - PQU |
928.28 km DAN - TATIM
- DADEN - MULAD - DONXO - POPET - KISAN -TRN |
941.42 km DAN - LATOM - DADEN - MULAD - KADUM
- POPET - KISAN - TRN |
Based
on the results from Figures 5, 6, and Table 1, it is evident that the model
operates accurately when identifying a new route to the newly designated
destination airport, which can be easily adjusted according to user needs. This
adaptability ensures that users can flexibly modify the destination based on
their specific needs without compromising the integrity of the routing process.
The model dynamically adjusts the path while maintaining computational
efficiency and consistency, making it highly suitable for real-world
applications. For the CRA - PQU route, the results from both runs of the model
are identical because the two waypoints, TATIM and DONXO, in the second result
do not belong to the original route. Consequently, their presence does not interfere
with the route calculation process, and the new path to the airport remains
unchanged. This highlights the robustness of the model in preserving optimal
paths when external constraints do not affect the original route structure.
However, for the DAN - PQU route, both TATIM and DONXO are integral parts of
the original route. As a result, in the second scenario, the alternative route
must also avoid these two waypoints, leading to an increase in the total travel
distance. This demonstrates the impact of waypoint constraints on the selection
of alternative ATS routes and highlights the model’s ability to navigate
complex restrictions to generate feasible and compliant alternative ATS routes.
The trade-off between distance and constraint adherence is evident in this
case, reinforcing the importance of considering waypoint dependencies in
routing optimization.
Next,
the results of the three scenarios for Case 2 are analyzed,
considering two distinct situations. Each situation involves two different No_fly_area. In the first situation, two No_fly_area are defined as polygons with the following:
(14.880556, 108.0197222), (14.479444, 107.8436111), (14.333333, 107.4000000),
(13.983333, 107.4166667), (13.957222, 109.0427778), (13.962500, 109.5213889),
(14.771389, 108.8075000) and (10.445278, 103.7763889), (10.895556,
105.2280556), (9.959444, 105.1330556), (8.500000, 104.0833333), (9.245000,
102.8383333). Upon their integration, the model identifies affected ATS routes
whose destination airports fall within these restricted zones. Notably, DAN–PQU
is impacted by both No-fly Areas, while CRA–PQU is affected by one. As a
result, rerouting to an alternate airport – assumed to be Côn
Sơn (CN) – is required. In Scenario 3, users may choose any point outside
the No-fly Area along the original route as the start_point
for diversion. Table 2 provides a comparative analysis of waypoint sequences
and route lengths, followed by Figures 7-10, which depict the corresponding
adjusted routes and waypoints.
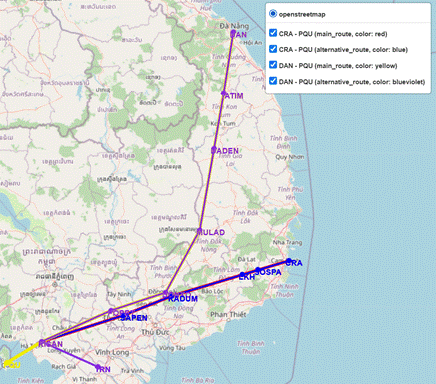
Fig. 5. Original and alternative Route
configurations when PQU becomes unavailable
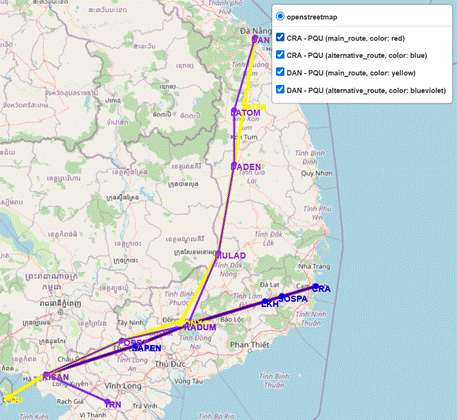
Fig. 6. Original and alternative Route
configurations when PQU, TATIM,
and DONXO becomes unavailable
Tab. 2
The detailed results of the
routes include a list of waypoints and lengths in Situation 1, Case 2
|
|
Original route |
Alternative route – Scenario 1 |
Alternative route – Scenario 2 |
Alternative route – Scenario 3 |
|
CRA – PQU |
602.243 km CRA - SOSPA - LKH - KADUM - SAPEN -
KISAN - PQU |
607.569 km CRA - SOSPA - LKH - KADUM - SAPEN -
BITIS - CN |
461.276 km CRA - ELSAS - CN |
484.146 km CRA - SOSPA
- LKH - RUTIT - ELSAS – CN |
|
DAN – PQU |
885.749 km DAN - TATIM
- DADEN - MULAD - DONXO - POPET - KISAN - PQU |
1216.229 km DAN - TATIM - KUMUN - VEPAM - KAMGO
- BMT - MULAD - DONXO - POPET - BITIS - CN |
989.815 km DAN - VEPAM
- KARAN - ELSAS - CN |
1130.605 km DAN - TATIM
- KUMUN - VEPAM - KAMGO - BMT - MULAD - DONXO - ESDOB - NIXIV – CN |
Fig. 7. The route analysis results are
influenced by Situation 1 of Case 2
and the newly input destination airport data
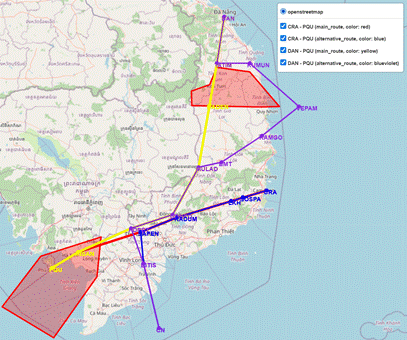
Fig. 8: Graphical results representing the
routes of Scenario 1, Situation 1, Case 2
In
the second situation, two No_fly_area were
established: one defined as a polygon with coordinates (16.2214, 107.6013),
(16.45264, 108.89553), (15.97414, 108.7921), and (15.6712, 107.8745), and
another as a circular area centered at (16.052778,
108.1983333) with a radius of 50 km. Notably, these two restricted areas have
overlapping regions. Following a similar approach as in the first situation,
the route assessment revealed that two routes, TSH-DAN and CRA-DAN, were
initially affected by the presence of these areas. As a result, an alternative
ATS route was required, with Chu Lai Airport (CQ) designated as the new
destination. In Scenario 3, the waypoints DADEN (TSH-DAN route) and KUMUN
(CRA-DAN route) were identified as key reference points for selecting
alternative ATS routes. Table 3 presents a comparative analysis of alternative
routing solutions, including waypoint sequences and route lengths, while
Figures 11-14 illustrate the route analysis results, new airport selection,
Scenario 3 starting point, and the adjusted route visualization.
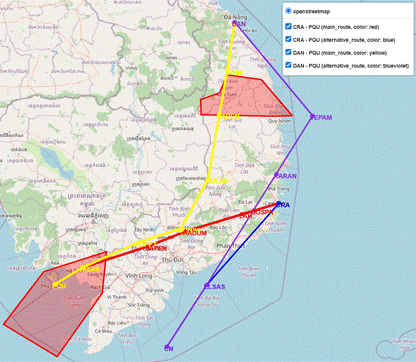
Fig. 9. Graphical results representing the
routes of Scenario 2, Situation 1, Case 2
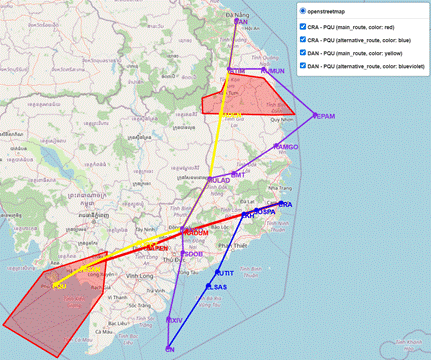
Fig. 10. Graphical results representing the routes
of Scenario 3, Situation 1, Case 2
Tab. 3
The detailed results of the
routes include a list of waypoints and lengths in Situation 2, Case 2
|
|
Original route |
Alternative route – Scenario 1 |
Alternative route – Scenario 2 |
Alternative route – Scenario 3 |
|
TSH – DAN |
612.169 km TSH - DONXO
- MULAD - DADEN - TATIM - DAN |
579.203 km TSH - DONXO
- MULAD - DADEN - TATIM - VILOT - SADIN - CQ |
557.747 km TSH - DONXO
- MULAD - MUMGA - CQ |
565.615 km TSH - DONXO
- MULAD - DADEN - BANSU – CQ |
|
CRA – DAN |
471.176 km CRA - KARAN - KAMGO - PCA - KUMUN -
DAN |
384.668 km CRA - KARAN - KAMGO - PCA - KUMUN -
CQ |
384.668 km CRA - KARAN - KAMGO - PCA - KUMUN -
CQ |
384.668 km CRA - KARAN - KAMGO - PCA - KUMUN –
CQ |
Fig. 11. The route analysis
results are influenced by Situation 2 of Case 2
and the newly input destination airport data
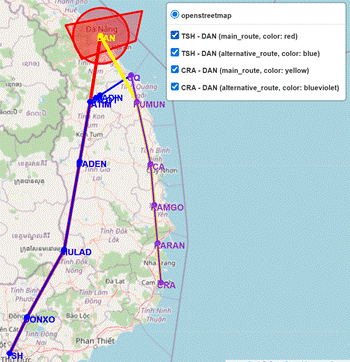
Fig. 12. Graphical results
representing the routes of Scenario 1, Situation 2, Case 2
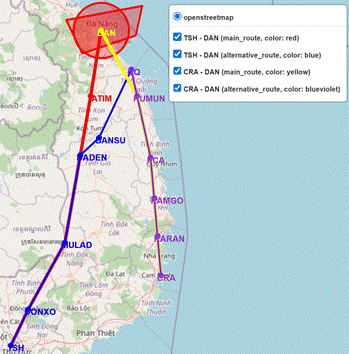
Fig. 13. Graphical results
representing the routes of Scenario 2, Situation 2, Case 2
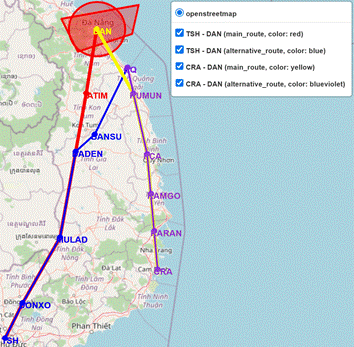
Fig. 14. Graphical results
representing the routes of Scenario 3, Situation 2, Case 2
The
analysis of results across all cases, including Case 1, highlights the model’s
remarkable flexibility and adaptability in selecting any airport as an
alternative destination. Regardless of the chosen replacement airport, the
model consistently generates accurate solutions that align with predefined
objective functions, ensuring operational feasibility and efficiency. This
adaptability is a key indicator of the model’s robustness, demonstrating its
capability to handle a wide range of operational constraints in dynamic ATM
environments.
A
more in-depth examination of the results in the two situations of Case 2
further confirms this observation. In both situations, all designed scenarios
are effectively fulfilled. Specifically, in Scenario 1, the alternative ATS
route closely follows the original ATS route, except for segments that require
modifications to bypass the No_fly_area, as well as
final adjustments necessary to reach the newly designated destination airport.
In Scenario 2, the selected ATS route consistently represents the shortest
among all feasible alternatives, confirming the model’s ability to identify
efficient alternative ATS routes. In Scenario 3, the model exhibits a high
degree of flexibility by dynamically determining the alternative ATS route
based on a user-specified start_point.
A
particularly noteworthy observation emerged in the case of the CRA–DAN route,
where the alternative ATS routes remained identical across all three scenarios.
This outcome can be attributed to the fact that No_fly_area
did not affect the initial segments of the original route. As a result, these
segments naturally formed the shortest possible path to the destination,
requiring no further optimization. This insight suggests that, in certain
cases, pre-existing route structures inherently align with optimal alternative
ATS route planning, thereby reducing the need for significant deviations.
Moreover,
the results obtained from Situation 1 and Situation 2 collectively reinforce
the model’s independence from the shape, size, and distribution of the No_Fly_area. Whether these areas are separate or
overlapping, the model consistently identifies the most suitable alternative
ATS route while ensuring compliance with airspace regulations. This
adaptability is crucial in complex airspace environments where restricted areas
may change dynamically due to geopolitical constraints, military operations, or
emergency airspace closures.
The
simulation results indicate that the model not only successfully identifies
alternative ATS routes but also ensures that these routes are operationally
feasible and compatible with all phases of ATFM. This is particularly critical
when one or more No_fly_area emerge due to both
unforeseen circumstances, such as adverse weather conditions, security threats,
or emergencies, and pre-planned situations, such as military exercises or
special airspace restrictions. These disruptions can significantly impact airport
operations and necessitate rapid aircraft diversions. Furthermore, the model
can be applied across different ATFM phases, particularly during the
pre-tactical stage, where planning and foresight are prioritized, and the
tactical stage, where flexibility and real-time adaptability are crucial for
responding to evolving situations. This capability is especially valuable in
high-traffic airspace environments, where maintaining efficiency and safety is
paramount. A key strength of the model lies in its high adaptability and
ability to dynamically optimize flight routes to accommodate operational
constraints. This demonstrates its practical applicability in ATM and
decision-making processes, contributing to enhanced efficiency, safety, and
resilience in airspace operations. In addition to enhancing the efficiency and
reliability of air traffic flows, the model contributes to reducing fuel
consumption and emissions by minimizing unnecessary detours and delays. This
aligns with broader goals of sustainable aviation and environmental
responsibility, further emphasizing its significance in modern ATM and
operational planning.
Overall,
the results confirm that the model performs reliably in alternative ATS routing
scenarios, demonstrating its effectiveness in addressing complex route planning
challenges. Its ability to adapt to changes while maintaining route
feasibility and efficiency makes it a powerful tool for applications requiring
dynamic navigation and optimized pathfinding under varying constraints.
4. CONCLUSION
Beyond
serving as a dynamic decision-support tool for identifying alternative ATS
routes when aircraft must divert to an alternate destination, this framework
can be effectively applied to a variety of operational scenarios, significantly
enhancing ATM efficiency and resilience. One of its key applications is the
development of contingency flight paths tailored to specific airspace regions
prone to frequent disruptions due to adverse weather conditions, high traffic
density, or unforeseen technical issues. By preemptively
designing such backup routes, air navigation service providers (ANSPs) can
ensure seamless operational continuity, minimizing delays and optimizing
airspace utilization under challenging circumstances. Furthermore, this model
can play a crucial role in enhancing trajectory-based operations (TBO) by
accurately determining real-time flight paths during various phases of
operation.
Importantly,
the implementation of alternative routing solutions in this model does not
require fundamental changes to existing airspace structures or control sectors.
Instead, it strategically utilizes current navigation aids, waypoints, and
predefined air traffic corridors, enabling a seamless integration within
existing ATM frameworks. This minimizes the need for costly infrastructural
overhauls while maximizing the effectiveness of available airspace resources.
This approach enhances flexibility and responsiveness while preserving the
integrity of established airspace management systems. By adopting this model,
ATC can proactively implement strategic decongestion measures, mitigating
bottlenecks and optimizing sector workload distribution while adhering to
established ATFM protocols. Moreover, the model enhances the capacity to
provide real-time guidance in response to unforeseen situations, ensuring
operational resilience. This adaptability is particularly valuable in
high-density airspace, where the ability to swiftly reassign flight paths
contributes to both safety and efficiency.
One
significant advantage of this model is its adaptability to various airspace
structures, achieved simply by modifying the input data, which consists of a
list of waypoint coordinates and airports within the designated airspace. This
flexibility allows for seamless integration into different ATM systems,
optimizing navigation efficiency across diverse operational environments. This
capability of the model ensures its applicability across a wide range of
scenarios, from managing low-density regional airspaces to handling
high-traffic international corridors. By dynamically adjusting to varying
airspace configurations, the model enhances route planning, minimizes
congestion, and contributes to the overall safety and efficiency of ATM.
Ultimately,
this approach significantly strengthens flight safety, enhances operational
predictability, and improves the adaptability of ATM systems without
necessitating structural changes to the FIR. By integrating such a framework,
ANSPs can modernize ATM operations, improve airspace utilization, and better
align with next-generation aviation initiatives. By leveraging these
advancements, the aviation industry can move toward a more intelligent ATM
model that ensures greater flexibility, dynamism, and adaptability in all
operational scenarios. This transformation is particularly crucial in an era of
increasing air traffic demand, evolving regulatory frameworks, and the
integration of emerging technologies such as artificial intelligence,
automation, and unmanned aerial systems.
References
1.
6Wresearch. 2024. "Vietnam aviation market
(2023-2029) outlook". Available at: https://www.6wresearch.com/industry-report/vietnam-aviation-market-outlook.
2.
Beeker E. 2004. "Potential error in the
reuse of Nilsson’s A algorithm for path-finding in military simulations". Journal
of Defense Modeling and Simulation 1(2). DOI: https://doi.org/10.1177/875647930400100203.
3.
Bongo M.F., C.L. Sy. 2020. "A robust optimisation formulation for post-departure rerouting
problem". In: Proceedings of the IEEE International Conference on
Industrial Engineering and Engineering Management: 509-513. DOI: https://doi.org/10.1109/IEEM45057.2020.9309827.
4.
Bureau of Transportation Statistics. 2025.
"On-time performance – Reporting operating carrier flight delays at a
glance". Available at: https://www.transtats.bts.gov/homedrillchart.asp.
5.
Carreras R., C. Greenman. 2025. "Vietnam’s
vision of growth in the aeronautical industry". Available at: https://commons.erau.edu/publication/740.
6.
Eurocontrol. 2024. "Cost of
diversion". Available at: https://ansperformance.eu/economics/cba/standard-inputs/chapters/cost_of_diversion.html#eurocontrol-recommended-values.
7.
Federal Aviation Administration. 2025.
"Airport benefit-cost analysis guidance". Available at: https://www.faa.gov/sites/faa.gov/files/regulations_policies/policy_guidance/benefit_cost/FAA_Airport_Benefits_Guidance.pdf.
8.
Felix Y.W., H.L.H.S. Warnars,
L.L.H.S. Warnars, A. Ramadhan, T. Siswanto. 2024.
"Searching routing using A-Star (A*) search algorithm". In: Proceedings
of the 3rd International Conference on Creative Communication and Innovative
Technology (ICCIT): 1-7. DOI: https://doi.org/10.1109/ICCIT62134.2024.10701177.
9.
Foead
D., A. Ghifari, B.M. Kusuma, N. Hanafiah, E. Gunawan.
2021. "A systematic literature review of A* pathfinding". Procedia
Computer Science 179: 507-514. DOI: https://doi.org/10.1016/j.procs.2021.01.034.
10. International
Trade Administration. 2024. "Aviation: Country commercial guide –
Vietnam". Available at: https://www.trade.gov/country-commercial-guides/vietnam-aviation.
11. Ji
Y., X. Wu, Y. Shang, H. Fu, J. Yang, W. Wu. 2024. "Unmanned ground vehicle
in unstructured environments applying improved A-star algorithm". In: Proceedings
of the 4th International Conference on Computer, Control and Robotics (ICCCR):
166-170. DOI: https://doi.org/10.1109/ICCCR61138.2024.10585482.
12. Ju
C., Q. Luo, X. Yan. 2020. "Path planning using an improved A-star
algorithm". In: Proceedings of the 11th International Conference on
Prognostics and System Health Management (PHM): 23-26. DOI: https://doi.org/10.1109/PHM-Jinan48558.2020.00012.
13. Kabir
R., Y. Watanobe, M.R. Islam, K. Naruse. 2024.
"Enhanced robot motion block of A-star algorithm for robotic path
planning". Sensors 24(5): 1422. ISSN: 1424-8220. DOI: https://doi.org/10.3390/s24051422.
14. Kurniawan
R., A. Armansyah, M. Idris. 2024. "Application
of artificial intelligence in the design of 2D Escape From Pirates game with A
Star algorithm search method". Jurnal
Dinda: Data Science, Information Technology, and Data Analysis 4(2). DOI: https://doi.org/10.20895/dinda.v4i2.1558.
15. Li
J., C. Yu, Z. Zhang, Z. Sheng, Z. Yan, X. Wu, W. Zhou, Y. Xie, J. Huang. 2023.
"Improved A-star path planning algorithm in obstacle avoidance for the
fixed-wing aircraft". Electronics 12(24): 5047. ISSN: 2079-9292.
DOI: https://doi.org/10.3390/electronics12245047.
16. Ma
L., H. Zhang, S. Meng, J. Liu. 2022. "Volcanic ash region path planning
based on improved A-star algorithm". Journal of Advanced Transportation.
DOI: https://doi.org/10.1155/2022/9938975.
17. Mandloi D., R. Arya,
A.K. Verma. 2021. "Unmanned aerial vehicle path planning based on A*
algorithm and its variants in 3D environment". International Journal of
System Assurance Engineering and Management 12: 990-1000. DOI: https://doi.org/10.1007/s13198-021-01186-9.
18. Neretin E.S., A.S. Budkov,
A.S. Ivanov. 2021. "Optimal four-dimensional route searching methodology
for civil aircrafts". In: Li B., C. Li, M. Yang, Z. Yan, J. Zheng (Eds.). IoT
as a Service 346: 433-442. Springer. DOI: https://doi.org/10.1007/978-3-030-67514-1_37.
19. Nguyen
Ngoc Hoang Quan, V.N. Nechaev, V.B. Malygin. 2025.
"Mathematical model and application of the A-star algorithm to optimize
ATS routes in the Area Control Center Ho Chi Minh airspace". Crede Experto: Transport, Society, Education, Language 1: 64-78.
ISSN: 2312-1327. DOI: https://doi.org/10.51955/2312-1327_2025_1_64.
20. OAG
Aviation Worldwide Limited. 2024. "The busiest flight routes of
2024". Available at: https://www.oag.com/busiest-routes-world-2024.
21. Roy
K.R. 2023. "Obstacle avoidance for quadcopters in formation flying based
on A* algorithm". In: Jain K., V. Mishra, B. Pradhan (Eds.). UASG 2021:
Wings 4 Sustainability 304: 443-456. Springer. DOI: https://doi.org/10.1007/978-3-031-19309-5_34.
22. Sathvik
N.G., S. Patil. 2021. "Performance analysis of Dijkstra’s and the A-star
algorithm on an obstacle map". In: Bhateja V., S.C. Satapathy, C.M. Travieso-González,
V.N.M. Aradhya (Eds.). Data Engineering and Intelligent Computing
1407: 81-90. Springer. DOI: https://doi.org/10.1007/978-981-16-0171-2_8.
23. VietnamPlus. 2025.
"Flights diverted, delayed due to bad weather at Tan Son Nhat
airport". Available at: https://en.vietnamplus.vn/flights-diverted-delayed-due-to-bad-weather-at-tan-son-nhat-airport-post253559.vnp.
24. Wang
Y., L. Qian, M. Hong, Y. Luo, D. Li. 2024. "Multi-objective route planning
model for ocean-going ships based on bidirectional A-star algorithm considering
meteorological risk and IMO guidelines". Applied Sciences 14(17):
8029. ISSN: 2076-3417. DOI: https://doi.org/10.3390/app14178029.
25. Xu
Y., R. Dalmau, M. Melgosa, A. Montlaur, X. Prats. 2020.
"A framework for collaborative air traffic flow management minimizing
costs for airspace users: Enabling trajectory options and flexible pre-tactical
delay management". Transportation Research Part B: Methodological
134: 229-255. DOI: https://doi.org/10.1016/j.trb.2020.02.012.
26. Yang
S., n Y. Ya, P. Chen. 2021. "Robust optimization models for flight
rerouting". International Journal of Computational Methods 18(5).
DOI: https://doi.org/10.1142/S0219876220400010.
Received 25.07.2025; accepted in revised form 30.10.2025
Scientific Journal of Silesian
University of Technology. Series Transport is licensed under a Creative
Commons Attribution 4.0 International License