Article citation information:

Karabulut, N.C. Application of response surface methodology to improve traffic signal performance and minimize lane inefficiency. Scientific Journal of Silesian University of Technology. Series Transport. 2025, 129, 97-114. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2025.129.6

Nihat Can KARABULUT[1]

APPLICATION OF RESPONSE SURFACE METHODOLOGY TO IMPROVE TRAFFIC SIGNAL PERFORMANCE AND MINIMIZE LANE INEFFICIENCY

Summary. Maintaining saturation flow at signalized intersections is crucial for both intersection capacity and sustainable traffic management. Efficient signal systems reduce congestion, lower emissions, and improve urban air quality. Factors such as signal timing, traffic demand, vehicle types, and intersection design significantly impact traffic flow efficiency. This study investigates the signal system and traffic flow parameters affecting lane inefficiency using Response Surface Methodology (RSM). Key factors included green time (G), the ratio of unused green time to total green time (ϴ/G), and discharge flow rate (β), while lane inefficiency (ẟ) served as the response variable. The full quadratic model was identified as the best model for explaining lane inefficiency due to its high adjusted R-squared value and low error values. The study recommends a green time of 30 seconds and a discharge flow rate of 0.540 vehicles per second per lane to obtain minimum lane inefficiency. These findings support decision-makers in creating smarter, more efficient signal-controlled intersections, ultimately contributing to sustainable urban transport infrastructure by improving traffic flow, reducing emissions, and lowering fuel consumption.

Keywords: fully actuated intersections, urban signal control, response surface methodology, lane inefficiency, optimization

1. INTRODUCTION

Efficient management of urban transportation networks is crucial for the sustainability and livability of cities. Improving traffic flow directly impacts the performance of transportation networks, making the management of urban intersections essential [1]. Well-designed and managed intersections reduce traffic congestion and increase road capacity, enhancing urban transportation efficiency [2]. Traffic signal control is a widely used strategy in intersection management, especially in developed cities [3].

Traditional fixed-time signal systems often fail to adapt to varying traffic conditions throughout the day [4]. To meet variable traffic demands, fully actuated signal control systems are becoming more popular. These systems dynamically adjust signal timings in real-time to minimize queue lengths and delays [5,6], significantly improving intersection capacity and overall traffic flow [7,8].

Optimizing intersection capacity relies on the saturation flow rate, a key element in traffic signal system planning [9]. Vehicles discharge at the saturation flow rate until the queue is fully dissipated [10]. The green extension period, following the clearance of queued vehicles, greatly influences signal control effectiveness. Research shows that discharge flow rates peak between 9 and 12 vehicles on straight lanes [11] but decrease after 40 to 60 seconds of green time [12]. Longer queue lengths have mixed effects on discharge flow rates [13].

Many factors affect the saturation flow rate, including intersection geometry, lane gradient, width and markings, vehicle composition, turning vehicles, pedestrian and bicycle activity, signal characteristics, weather conditions, signal countdown devices, and autonomous vehicles [14-21]. Despite extensive research, few studies focus on saturation flow rate fluctuations at fully actuated intersections.

To address this gap, Karabulut et al. [22] introduced a lane inefficiency parameter to provide insights into vehicle discharge efficiency at the saturation flow rate during the green period at fully actuated intersections. In this study, the lane inefficiency parameter was modeled in a quadratic form using the Response Surface Methodology (RSM). The RSM optimization technique was employed to identify optimal values of key factors to minimize lane inefficiency. The primary aim is to minimize lane inefficiency by understanding the factors affecting the performance of fully actuated intersections. The novelty of this approach lies in applying RSM to model and optimize lane inefficiency. This not only enhances the understanding of influencing factors but also provides a practical framework for improving intersection performance. The benefits include better traffic flow management, reduced congestion, and enhanced road capacity at signal-controlled intersections. The structure of this study is as follows: Section 2 outlines the study area and data collection methods. Section 3 details the research methodology. Section 4 presents the modeling and optimization results. Section 5 summarizes the key conclusions.

2. STUDY AREA AND DATA

For this study, traffic flow data were collected from two urban intersections, Expo and Mall, in Mersin, Turkey. Table 1 shows the geometric and traffic flow characteristics of these intersections, which are controlled by fully actuated traffic signals. Traffic video recordings of the approach legs at these intersections were obtained from the Transportation Department of the Mersin Metropolitan Municipality. These recordings were made during the morning peak hours on two weekdays under normal weather conditions. Signalization system data, including the start and end times of the green and red periods for each signal cycle, were also collected. During the morning peak hours, high traffic volumes were observed on the West, East, and North approaches of the Mall intersection, and on the West approach of the Expo intersection (see Table 2). Approaches with low traffic volumes were not included in the study. Images captured from the examined approaches are shown in Fig. 1.

Tab. 1

General attributes of Mall and Expo intersections

Attributes	Mall	Expo
Intersection type	Roundabout	Four-leg
Signalization type	Fully actuated	Fully actuated
Number of approach leg	4	4
Number of lanes	3	3
Lane width	3.0-3.6 m	3.0-3.6 m
Lane slope	2%	2%
Traffic composition	Mixed	Mixed
Pedestrian activity	Limited	Limited

Tab. 2

Observed traffic volumes

Intersection	Approach	Day 1 (07:30-09:30)			Day 2 (07:30-09:30)
		Left	Middle	Right	Left	Middle	Right
Mall	West	1,077	3,052	1,826	1,120	2,819	1,892
	East	266	2,192	1,727	278	2,314	1,548
	North	730	1,006	452	460	1,224	456
Expo	West	1,454	1,799	400	1,091	2,279	281

Fig. 1. Studied intersection approaches

3. METHODOLOGY

As previously mentioned, the saturation flow rate is essential for maximizing intersection capacity and plays a vital role in the planning and design of traffic signal systems [9]. During the queue service time, vehicles discharge at this flow rate until the queue is completely cleared [10]. The green extension period following the discharge of queued vehicles is critical for the effectiveness of signal control. Ensuring optimal performance of signal control systems involves facilitating vehicle discharges at the saturation flow rate during this extension period.

In a previous study, Karabulut et al. [22] introduced the lane inefficiency parameter to provide a more detailed understanding of vehicle discharge effectiveness during the green period at intersections with fully actuated signal systems. This parameter is calculated by comparing the saturation flow rate with the instantaneous discharge rate for each green period, offering a comprehensive assessment of green utilization for specific lanes. Specifically, Fig. 2 shows the instant discharge flow rate during two green periods where the number of queued vehicles is 11 and green time is 38 seconds. The saturation flow rates were calculated as 0.43 vehicles per second per lane using the HCM [23] methodology. During the first green period, most vehicles discharged at or near the saturation flow rate. However, this efficiency was not maintained during the second green period. In this context, the developed lane inefficiency parameter (δ) offers insights into the effectiveness of vehicle discharge at the saturation flow rate during the green period by comparing instant discharge rates with the saturation flow rate. The mathematical analysis results indicated that the lane inefficiency value was 3.3% for the first green period and 24.7% for the second. Indicating that 3.3% and 24.7% of the (G-t₁) period were used inefficiently, respectively. G is the green time and t1 is the initial loss time which was set at 2 seconds in line with recommendations from the HCM [23]. This situation clearly indicates that the efficiency of traffic flow duration cannot be evaluated solely based on the saturation flow rate value or number of discharged vehicles.

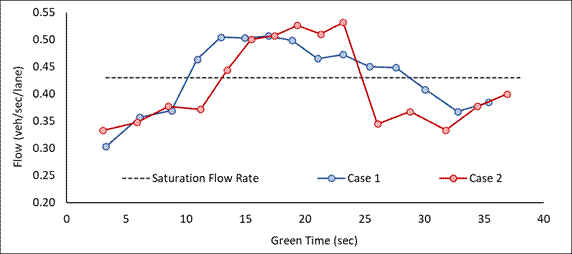
Fig. 2. Studied intersection approaches

In this study, the lane inefficiency parameter developed by Karabulut et al. [22] was modeled using the Response Surface Methodology (RSM) technique. Subsequently, the RSM optimization technique was employed to determine the optimal values of key factors to minimize lane inefficiency. During the RSM process, careful consideration was given to include both traffic flow and traffic signal system parameters. Therefore, green time (G), the ratio of unused green time to total green time (ϴ/G), and discharge flow rate (β) were chosen as factors, while lane inefficiency (ẟ) was used as the response variable (see Fig. 3).

The flowchart of the proposed methodology is presented in Fig. 3. As seen, three factors and one response were considered. The green time (G) refers to the portion of a signal phase in which the green signal is illuminated. The ratio of total unused green time to green time (Ɵ/G) is the percentage expression of the ratio of total unused green time (Ɵ) to displayed green time (G) in a signal phase. The discharge flow rate (β) refers to the average time headway of the vehicles traversing the stop line during the green period. An example of table building is shown below for Tab. 1.

Central composite design (CCD) was employed to analyze the effects of the selected factors on lane inefficiency (ẟ) response (see Fig. 3). The CCD procedure involves systematically examining the effects of different factor values on the response. For this purpose, mathematical models containing linear, quadratic, and interaction terms were formulated based on field observation data. Among these models, the one that best represents the relationship between factors and response was selected. Subsequently, contour graphs were generated to observe the variation of lane inefficiency (ẟ) with different values of factors. In the final step, optimization was conducted to determine the factor values that minimize the lane inefficiency response.

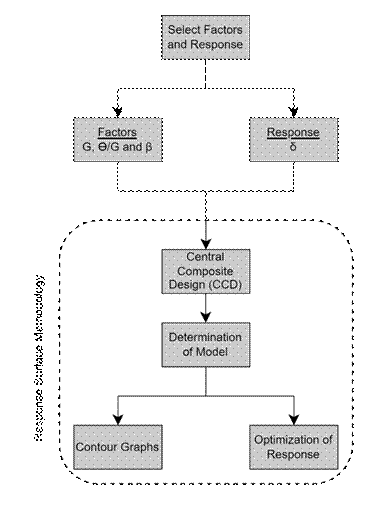
Fig. 3. The flow chart of the proposed methodology

3.1. Response Surface Methodology

Response Surface Methodology (RSM) is a mathematical and statistical technique valuable for the development, enhancement, and optimization of processes [24]. Compared to traditional experimental and optimization methods, RSM offers numerous advantages. It efficiently extracts significant information from a limited number of experiments using diverse experimental designs, setting it apart from other techniques [25]. Moreover, RSM evaluates the interaction effects of factors on the response variable, making it an invaluable tool for modeling and optimizing problems.

RSM offers different experimental approaches, with one standout being the central composite design (CCD). Developed by Box and Wilson (1951), CCD is recognized as a premier second-order design in literature. It enhances the initial first-order design, typically composed of n factors, by incorporating additional axial points, factorial points, and center points. This expansion allows for a thorough exploration of the response surface, making CCD a popular choice in many studies. In a standard CCD with n factors, the factorial points (βf), also known as cube or corner points, are coded at levels of ±1. The total number of factorial points is determined by 2n. Meanwhile, the center point (βc) is coded as zero and serves to evaluate model fit. Axial points (βa) are placed at a specified distance α from the design center in each coded factor level direction. The count of axial points in the experimental setup can be calculated using the formula 2n. For visual reference, Fig. 4 illustrates a CCD designed for 3 factors.

In this study, as mentioned above, to model lane inefficiency response, three factors were considered: green time (G), the ratio of total unused green time to green time (Ɵ/G), and discharge flow rate (β). The CCD for these three factors requires a total of 20 experiments, which correspond to cycles of the signalization system. These experiments were randomly selected from field observations and included 8 factorial points, 6 axial points, and 6 central points (see Table 3). An axial length of 1.68179 was chosen based on the number of factorial points. Factorial points were coded with levels of ±1, axial points with levels of ±1.68179, and center points with a level of 0. Each factor exhibited three different levels, as depicted in Table 4.

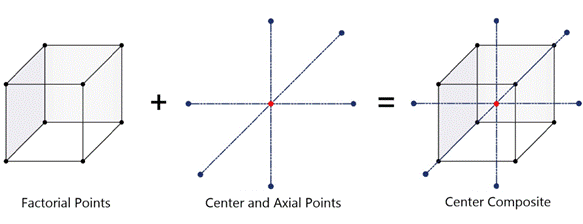
Fig. 4. CCD for 3 factors

Tab. 3

Factors and response values of the randomly selected experiments

Observations	Model factors values
	Coded value			Uncoded value			Response
	G	ϴ/G	β	G	ϴ/G	Β	ẟ
1	-1	1	-1	30	4.48	0.538	7.22
2	1	1	-1	33	5.54	0.505	13.99
3	1	-1	1	33	5.90	0.499	16.34
4	1.68179	0	0	32	6.84	0.539	8.88
5	0	0	0	30	4.85	0.508	10.99
6	0	0	0	47	14.84	0.391	33.10
7	-1	-1	1	35	11.37	0.345	23.45
8	1	-1	-1	35	12.88	0.469	24.36
9	0	0	0	35	10.10	0.373	25.02
10	0	0	0	52	9.93	0.421	35.46
11	0	1.68179	0	48	22.20	0.422	35.68
12	0	0	1.68179	66	18.35	0.449	36.37
13	0	0	0	50	10.01	0.378	33.12
14	0	0	-1.68179	68	18.78	0.443	33.67
15	1	1	1	68	18.83	0.406	34.90
16	-1.68179	0	0	50	9.12	0.369	34.98
17	0	0	0	62	20.07	0.363	39.93
18	0	-1.68179	0	43	19.20	0.384	37.45
19	-1	1	1	61	9.51	0.438	38.35
20	-1	-1	-1	68	15.15	0.319	38.70

G (sec); ϴ/G (%); β (veh/sec/lane); ẟ (%)

Tab. 4

Level of factors for CCD

Factors	Levels
	-1.68179	0	1.68179
Green time (G)	30	49	68
Total unused green time/Green time (ϴ/G)	4.48	13.34	22.20
Discharge flow rate (β)	0.32	0.43	0.54

G (sec); ϴ/G (%); β (veh/sec/lane)

4. RESULTS

In accordance with the methodology developed by Karabulut et al. [22], lane inefficiency was calculated for 239 green periods. The traffic flow properties of these green periods are shown in Table 5. For example, at the West approach of the Mall intersection, the average green time is 56 seconds, with a saturation flow rate of 0.574 vehicles per second per lane and a discharge flow rate of 0.486 vehicles per second per lane. The average queue length on this approach is 10.6 vehicles per cycle per lane. The traffic composition comprises passenger cars (PC) at 92.2%, public transport (PT) at 2.4%, and heavy vehicles (HV) at 5.4%. These parameters offer valuable insights into traffic patterns, congestion levels, and vehicle composition, aiding in traffic management and optimization efforts.

Tab. 5

Properties of the studied green periods

Intersection		Mall			Expo
Approach		West	East	North	West
Studied green periods		93	38	52	56
Green time (sec)	Min.	31	19	20	18
	Avg.	56	32	25	23
	Max.	72	35	30	33
Saturation flow rate (veh/sec/lane)	Min.	0.416	0.406	0.404	0.395
	Avg.	0.525	0.493	0.559	0.574
	Max.	0.741	0.673	0.735	0.874
Discharge flow rate (veh/sec/lane)	Min.	0.319	0.345	0.390	0.373
	Avg.	0.435	0.422	0.466	0.486
	Max.	0.520	0.492	0.578	0.522
Queue length (veh/cycle/lane)	Min.	8	8	8	8
	Avg.	14.0	11.0	10.0	10.6
	Max.	25	15	15	15
Traffic composition (%)	PC	94.3	92.2	97.3	92.5
	PT	4.6	2.4	2.7	5.1
	HV	1.1	5.4	0.0	2.4

4.1. Response Modeling

To investigate the relationship between factors (G, Ɵ/G, and β) and lane inefficiency (δ) (response variable), four different RSM models have been developed (see Table 6). Note that, as mentioned above, lane inefficiency was calculated for 239 green periods, and 20 of these were randomly selected to be used in the developed models. Model 1 exclusively considers the linear effects of factors on lane inefficiency (δ) response (see Eq. 1). The equation of this linear model indicates that lane inefficiency (δ) response increases with an increase in green time (G) and the ratio of total unused green time to green time (Ɵ/G). Conversely, lane inefficiency (δ) response increases as discharge flow rate (β) factors decrease. The linear model exhibits an adjusted R-square value of 0.852 (see Table 6).

(1)

Model 2 incorporates both the linear and square effects of factors (see Eq. 2). The equation of the model demonstrates that the linear and square terms of factors exert distinct effects on lane inefficiency (δ) response. While the linear terms exhibit positive effects, the square terms demonstrate negative effects. Model 2 achieves an adjusted R-square value of 0.964 (see Table 6).

(2)

Model 3 incorporates the linear and interaction effects of factors (see Eq. 3). Both green time (G) and the ratio of total unused green time to green time (Ɵ/G) exhibit a positive effect, whereas the discharge flow rate (β) demonstrates a negative effect. Additionally, the interaction terms G*(Ɵ/G) and β*(ϴ/G) show negative effects, while the interaction term (G*β) displays a positive effect. Model 3 has an adjusted R-squared value of 0.955 (see Table 6).

(3)

Model 4 is a full quadratic model that includes linear, square, and interaction terms of the factors (see Eq. 4). The linear terms contribute positively to the lane inefficiency response, whereas the interaction terms exert a negative impact on it. Specifically, only (Ɵ/G)² among the squared terms demonstrates a positive effect, while the other quadratic terms yield a negative effect. The adjusted R-squared value of Model 4 is 0.980 (see Table 6).

(4)

The analysis reveals that the full quadratic model demonstrates the highest adjusted R-square value and the smallest absolute residuals (see Table 6). Consequently, the full quadratic was selected, as it provides the best overall fit and statistical performance among the tested models. The ANOVA results presented in Table 7 indicate that the terms (linear, square, and interaction) of the full quadratic model are significant at a 95% significance level. Examination of the residual values of the full quadratic model, depicted in Fig. 5 and 6, shows that the predicted values closely align with the actual values, confirming the model's effectiveness.

Tab. 6

R-square values of the developed models

Model	Model type	R-square		Residual
		R^2	R^2(adj)	Min.	Max.
1	Linear	0.875	0.851	-5.58	7.31
2	Linear and square	0.974	0.961	-2.44	3.51
3	Linear and interaction	0.969	0.955	-3.97	2.91
4	Full quadratic	0.989	0.980	-2.31	2.36

Tab. 7

ANOVA results of full quadratic model

Source	Degree of freedom	Sum of squares (adj)	Mean squares (adj)	F-value	p-value	Remarks
Model	9	2255.89	250.65	102.20	0.000	Sig.
Linear terms	3	751.20	250.40	102.09	0.000	Sig.
Square terms	3	46.07	15.36	6.26	0.012	Sig.
Interactions terms	3	35.95	11.98	4.89	0.024	Sig.

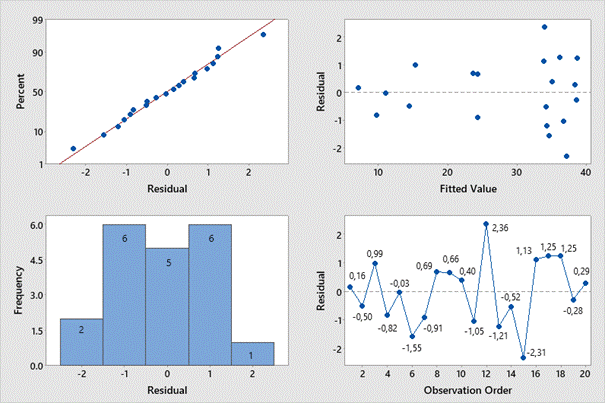
Fig. 5. Residual values of the full quadratic model

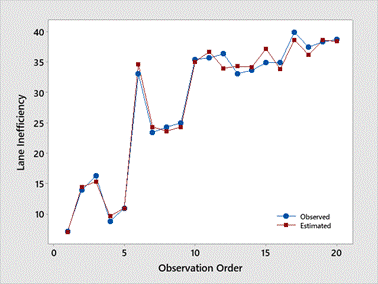
Fig. 6. Observed and estimated values for the quadratic model

After selecting the quadratic model, contour graphs were created to visualize how lane inefficiency (ẟ) changes with different values of the factors. Fig. 7 illustrates the impact of green time (G) and the ratio of total unused green time to green time (Ɵ/G) on lane inefficiency response, with a constant discharge flow rate (β) of 0.43 vehicles per second per lane, which is the observed average value (see Table 4). It is evident that longer green times (G) and higher ratios of total unused green time to green time (Ɵ/G) have adverse effects on lane inefficiency (ẟ).

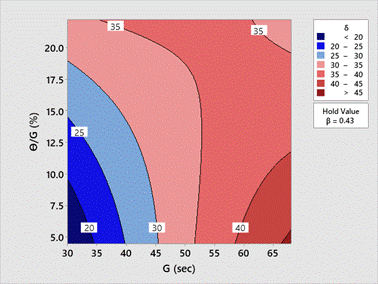
Fig. 7. Contour graphs of G and Ɵ/G

The second contour graph illustrates the effects of green time (G) and discharge flow rate (β) on lane inefficiency response, with a constant ratio of total unused green time to green time (Ɵ/G) at 13.34%, which is the observed average value (see Table 4). At longer green times (G) and lower discharge flow rate (β) values, the maximum lane inefficiency (ẟ) response is observed (see Fig. 8). This result reinforces the previous finding, indicating that the longer green time (G) parameter negatively affects lane inefficiency (ẟ) response.

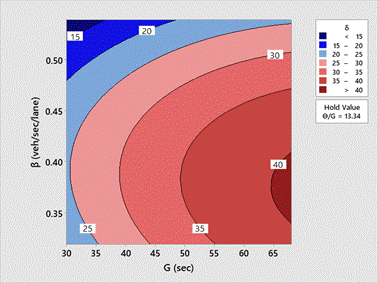
Fig. 8. Contour graphs of G and β

The latest contour graph illustrates how the ratio of total unused green time to green time (Ɵ/G) and the discharge flow rate (β) influence lane inefficiency (ẟ), while keeping the green time (G) constant at 49 seconds, which is the observed average value (see Table 4). The highest lane inefficiency (ẟ) occurs at a higher ratio of total unused green time to green time (Ɵ/G) and a lower discharge flow rate (β) (see Fig. 9). It can be concluded that the discharge flow rate (β) demonstrates an inverse relationship with lane inefficiency (ẟ) response. This means that as the discharge flow rate decreases, lane inefficiency tends to increase, particularly when there is a higher proportion of total unused green time to green time.

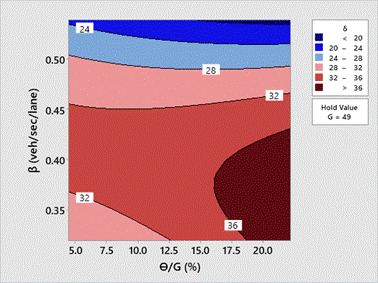
Fig. 9. Contour graphs of Ɵ/G and β

4.2. Response Optimization

In the final phase of the study, the Response Surface Methodology (RSM) was employed to optimize the lane inefficiency (ẟ) response, with the aim of minimizing it. The optimization process sought to identify factor values that yield the lowest lane inefficiency. To achieve this, a desirability function was defined during the optimization. The desirability function (D) is used to assess how close the response is to the target value [24]. The highest desirability value is 1, indicating the optimal response, while the lowest is 0. In this study, the desirability function was set to 1. Additionally, to minimize the lane inefficiency (ẟ) response, the weights and importance levels of the factors were also defined as 1.

The graphs obtained for the optimum values of the factors are shown in Fig. 10. They indicate that the lane inefficiency (ẟ) response increases as the green time (G) and the ratio of total unused green time to green time (Ɵ/G) increase. It also shows that the lane inefficiency (ẟ) response decreases as the discharge flow rate (β) increases. Additionally, the optimization graph suggests a green time of 30 seconds, a ratio of total unused green time to green time (Ɵ/G) of 5%, and a discharge flow rate of 0.540 vehicles per second per lane to minimize lane inefficiency. By providing these values, the lane inefficiency response will be 6.94% (see Fig. 10).

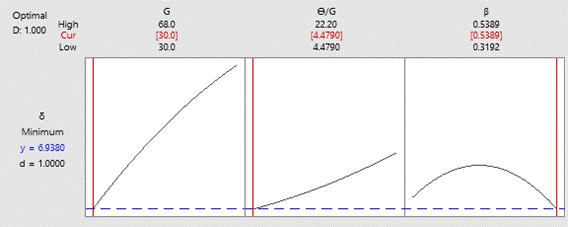
Fig. 10. Optimization graphs of lane inefficiency (ẟ) response

5. CONCLUSIONS

Maintaining saturation flow at signalized intersections is very important for both intersection capacity and sustainable traffic management. Efficient signal systems help to reduce congestion, lower emissions, and improve air quality in cities. Factors like signal timing, traffic demand, vehicle types, and intersection design have a big impact on traffic flow efficiency. By optimizing these elements, traffic engineers can improve intersection performance, resulting in smoother traffic flow and fewer delays.

Recently, Karabulut et al. [22] introduced a new parameter called lane inefficiency to assess how well vehicles discharge during green periods at fully actuated intersections. In this study, signal system and traffic flow parameters affecting lane inefficiency were studied using Response Surface Methodology (RSM). In the developed methodology, green time (G), the ratio of unused green time to total green time (ϴ/G), and discharge flow rate (β) were chosen as factors, while lane inefficiency (ẟ) was used as the response variable. RSM was chosen because it can model and optimize the relationship between the response and factors very well. The best model for explaining lane inefficiency was a full quadratic model, which had the highest adjusted R-squared value and the lowest error values.

It is essential to operate intersections with these optimal values to reduce inefficiency and improve performance. Minimizing the initial vehicles' lost time in the queue, ideally losing no more than 5% of the green time, is crucial for maintaining efficient traffic flow. It was observed that vehicle headways and time losses increased after the 25th second of green time, leading to reduced discharge flow rates. Consequently, the optimization process recommended a green time of 30 seconds and a discharge flow rate of 0.540 vehicles per second per lane to minimize lane inefficiency.

The results of this study go beyond the specific intersections analyzed, showing that RSM is a good technique for traffic engineering. The lane inefficiency parameter helps understand signal dynamics at fully actuated intersections and provides recommendations for optimizing traffic signal timing, reducing environmental impact, and maintaining saturation flow rates. This directly helps the sustainable use of urban transport infrastructure. The study highlights the dynamic relationship between green time and lost time, giving practical insights for decision-makers to improve traffic flow efficiency, reduce emissions, and lower fuel consumption. By optimizing green times, the study achieves the goals of efficient and environmentally friendly urban transportation. The analysis and recommendations can be adapted to different urban contexts, promoting sustainable urban transport infrastructure on a broader scale.

Appendix: Computing of Lane Inefficiency Parameter

In this section, lane inefficiency methodology and example calculation are explained in detail. As an example, Fig. 2 depicted the instant discharge flow rate (β_j) (veh/sec) and saturation flow rate (S) (veh/sec) during the green period. The instant discharge flow rate (β_j) (veh/sec) was calculated using the time headways of the vehicles that pass the stop line during the green period (see Eq. 5).

(5)

where j refers to the j^th vehicle that passes the stop line during the green period, and h_j refers to the time headway of the j^th vehicle (see Fig. 2).

The HCM method enables the calculation of the saturation flow rate for each green period. Therefore, the saturation flow rate (S) was calculated separately for each green period by Eq. 6.

(6)

where refers to the saturated headway (sec/veh) for the green period. The saturated headway () was calculated by Eq. 7, where n refers to the total number of vehicles in a queue, and h_q refers to the time headway of q^th vehicle in a queue.

(7)

As depicted in Fig. 2, the instant discharge rate (β_j) fluctuates during the green period, and inefficiency arises when the instant discharge rate (β_j) drops below the saturation flow rate (S). The total inefficiency during the green period consists of the following three components: a) the inefficiency resulting from the initial unused green time (), b) the inefficiency resulting from the unused green time after the last vehicle passes the stop line (), c) the sum of inefficiency resulting from the low instant discharge flow rate (). The total inefficiency is equal to:

(8)

where was calculated by Eq. 9.

(9)

where refers to the initial unused green time (sec.) for the green period was calculated by Eq. 10.

(10)

where refers to the time headway of the first vehicle in the queue. refers to the initial loss time, which was taken as 2 seconds in line with the recommendations from the HCM 2010 (TRB, 2010). The inefficiency resulting from the unused green time after the last vehicle () was calculated by Eq. 11.

(11)

where refers to the unused green time after the last vehicle (sec.) and was calculated by Eq. 12.

(12)

where G refers to the green time (sec.), and m is the departure volume for the green period (i.e., number of vehicles that pass the stop line during the green period).

The sum of inefficiency resulting from the low instant discharge flow rate () was calculated by an algorithm developed in MATLAB.

Conversely, surpassing the instantaneous discharge rate (β_j) above the saturation flow rate () signifies efficiency (oversaturation). It's equally important to take these efficient segments into account during a green period. Therefore, clear inefficiency during the green time can be expressed by Eq. 13.

(13)

where refers to the clear inefficiency, and refers to the total efficiency during the green period. The total efficiency resulting from oversaturation was calculated by an algorithm developed in MATLAB.

If Eq. 8 to 13 are closely examined, the unit of the and parameters is vehicle. Therefore, clear inefficiency () corresponds to the number of unserved vehicles within traffic flow as a result of unmaintainable saturation flow during the green period. Accordingly, lane inefficiency () of the green period can be calculated by Eq. 14.

(14)

As an example, the lane inefficiency of any green period can be calculated as follows:

The green period was 46 seconds (). The first vehicle in the queue traversed the stop line 2.949 seconds after the start of green (). The green period finished 3.951 sec after the last vehicle traversed the stop line (). The saturation flow rate of the green period was calculated as 0.449 veh/sec/lane ().

Therefore:

seconds

vehicles

vehicles

vehicles (calculated from MATLAB)

vehicles

=1.961 vehicles (calculated from MATLAB)

The total efficient area is subtracted from the total inefficient area of the cycle. The clear inefficient area of the cycle is determined.

vehicles

22.23% of the () period was used inefficiently.

References

1. Cipriani Ernesto, Livia Mannini, Barbara Montemarani, Marialisa Nigro, Marco Petrelli. 2019. „Congestion pricing policies: Design and assessment for the city of Rome, Italy”. Transport Policy 80: 127-135. ISSN: 1879-310X. DOI: https://doi.org/10.1016/j.tranpol.2018.10.004.

2. Mondal Satyajit, Ankit Gupta. 2020. „A review of methodological approaches for saturation flow estimation at signalized intersections”. Canadian Journal of Civil Engineering 47(3): 237-247. DOI: https://doi.org/10.1139/cjce-2018-0696.

3. Wong S.C., N.N. Sze, Y.C. Li. 2007. „Contributory factors to traffic crashes at signalized intersections in Hong Kong”. Accident Analysis & Prevention 39(6):1107-1113. ISSN: 1879-2057. DOI: https://doi.org/10.1016/j.aap.2007.02.009.

4. Gong Yue-Jiao, Jun Zhang. 2014. „Real-time traffic signal control for modern roundabouts by using particle swarm optimization-based fuzzy controller”. arXiv: 1408.0689. DOI: https://doi.org/10.48550/arXiv.1408.0689.

5. Cai Chen, Chi Kwong Wong, Benjamin G. Heydecker. 2009. „Adaptive traffic signal control using approximate dynamic programming”. Transportation Research Part C: Emerging Technologies 17(5): 456-474. ISSN: 1879-2359. DOI: https://doi.org/10.1016/j.trc.2009.04.005.

6. Mohammed Ali Muzamil Eltejani, Akif Durdu, Seyit Alperen Çeltek, Alper Yılmaz. 2021. „An adaptive method for traffic signal control based on fuzzy logic with webster and modified webster formula using SUMO traffic simulator”. IEEE Access 9: 102985-102997. ISSN: 2169-3536. DOI: https://doi.org/10.1109/ACCESS.2021.3094270.

7. Fan Jieyu, Arsalan Najafi, Jokhio Sarang, Tian Li. 2023. „Analyzing and Optimizing the Emission Impact of Intersection Signal Control in Mixed Traffic”. Sustainability 15(22): 16118. ISSN: 2071-1050. DOI: https://doi.org/10.3390/su152216118.

8. Majstorović Željko, Leo Tišljarić, Edouard Ivanjko, Tonči T. Carić. 2023. „Urban traffic signal control under mixed traffic flows: Literature review”. Applied Sciences 13(7): 4484. ISSN: 2076-3417. DOI: https://doi.org/10.3390/app13074484.

9. Du Yu, Anastasios Kouvelas, Wei ShangGuan, Michail A Makridis. 2022. „Dynamic capacity estimation of mixed traffic flows with application in adaptive traffic signal control”. Physica A: Statistical Mechanics and its Applications 606: 128065. ISSN: 1873-2119. DOI: https://doi.org/10.1016/j.physa.2022.128065.

10. Zheng Xing, Will Recker, Lianyu Chu. 2010. „Optimization of control parameters for adaptive traffic-actuated signal control”. Journal of Intelligent Transportation Systems 14(2): 95-108. DOI: https://doi.org/10.1080/15472451003719756.

11. Li Honglong, Panos D. Prevedouros. 2002. „Detailed observations of saturation headways and start-up lost times”. Transportation Research Record 1802(1): 44-53. ISSN: 0361-1981. DOI: https://doi.org/10.3141/1802-06.

12. Khosla Karan, James C. Williams. 2006. „Saturation flow at signalized intersections during longer green time”. Transportation research record 1978(1):61-67. ISSN: 0361-1981. DOI: https://doi.org/10.1177/0361198106197800109.

13. Gao L., B. Alam. 2014. „Optimal discharge speed and queue discharge headway at signalized intersections”. In: 93rd Annual Meeting of Transportation Research Board. Washington, DC, United States.

14. Chen Peng, Hideki Nakamura, Miho Asano. 2011. „Saturation flow rate analysis for shared left-turn lane at signalized intersections in Japan”. Procedia-Social and Behavioral Sciences 16: 548-559. ISSN: 1877-0428. DOI: https://doi.org/10.1016/j.sbspro.2011.04.475.

15. Shao Chang-qiao, Jian Rong, Xiao-ming Liu. 2011. „Study on the saturation flow rate and its influence factors at signalized intersections in China”. Procedia-Social and Behavioral Sciences 16: 504-514. ISSN: 1877-0428. DOI: https://doi.org/10.1016/j.sbspro.2011.04.471.

16. Potts Ingrid, John F. Ringert, Karin M. Bauer, John D. Zegeer, Douglas W. Harwood, David K. Gilmore. 2007. „Relationship of lane width to saturation flow rate on urban and suburban signalized intersection approaches”. Transportation research record 2027(1): 45-51. ISSN: 0361-1981. DOI: https://doi.org/10.3141/2027-06.

17. Seyed Rasoul Davoodi, Saman Sadeghiyan, Seyed Farzin Faezi. 2015. „The analysis the role of motorcycles on saturation flow rates at signalized intersections in Gorgan”. Indian Journal of Science and Technology 8(13): 1-6.

18. Wang Yi, Jian Rong, Chenjing Zhou, Yacong Gao. 2020. „Dynamic estimation of saturation flow rate at information-rich signalized intersections”. Information 11(4): 178. ISSN: 2078-2489. DOI: https://doi.org/10.3390/info11040178.

19. Mondal Satyajit, Ankit Gupta. 2021. „Non-linear evaluation model to analyze saturation flow under weak-lane-disciplined mixed traffic stream”. Transportation Research Record 2675(8): 422-431. ISSN: 0361-1981. DOI: https://doi.org/10.1177/0361198121998370.

20. Lu Zhengyang, Tae J. Kwon, Liping Fu. 2019. „Effects of winter weather on traffic operations and optimization of signalized intersections”. Journal of traffic and transportation engineering 6(2): 196-208. ISSN: 2589-0379. DOI: https://doi.org/10.1016/j.jtte.2018.02.002.

21. Liu Xinyu, Jie Yu, Xiaoguang Yang. 2021. „Diagnostic-oriented and evaluation-driven framework for bus route performance improvement”. Journal of Transportation Engineering, Part A: Systems 147(6): 04021030. ISSN: 2473-2893. DOI: https://doi.org/10.1061/JTEPBS.0000521.

22. Nihat Can Karabulut, Murat Ozen, Oruc Altintasi. 2024. „Understanding the Determinants of Lane Inefficiency at Fully Actuated Intersections: An Empirical Analysis”. Sustainability 16(2): 722. ISSN: 2071-1050. DOI: https://doi.org/10.3390/su16020722.

23. Transportation Research Board (TRB). 2010. Highway capacity manual (5th Edition). Washington, D.C. Transportation Research Board, National Research Council.

24. Myers R.H., D.C. Montgomery, C.M. Anderson-Cook. 2016. Response surface methodology: process and product optimization using designed experiments. John Wiley & Sons.

25. Baş Deniz, İsmail H. Boyacı. 2007. „Modeling and optimization I: Usability of response surface methodology”. Journal of food engineering 78(3): 836-845. ISSN: 1873-5570. DOI: https://doi.org/10.1016/j.jfoodeng.2005.11.024.

Received 13.07.2025; accepted in revised form 05.10.2025

Scientific Journal of Silesian University of Technology. Series Transport is licensed under a Creative Commons Attribution 4.0 International License

---

[1] Faculty of Civil Engineering, Yıldız Technical University, Istanbul, Turkey. Email: can.karabulut@std.yildiz.edu.tr. ORCID: https://orcid.org/0000-0002-4294-0215