Article
citation information:
Betin,
D., Koloskova, H., Betin, O. Influence of altitude-velocity
limitations of physical modelling problems on the main parameters of free
flying aircraft models. Scientific
Journal of Silesian University of Technology. Series Transport. 2025, 128, 71-81. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2025.128.4
Denys BETIN[1],
Hanna KOLOSKOVA[2],
Olexander BETIN[3]
INFLUENCE OF
ALTITUDE-VELOCITY LIMITATIONS OF PHYSICAL MODELLING PROBLEMS ON THE MAIN
PARAMETERS OF FREE FLYING AIRCRAFT MODELS
Summary. Reducing the time and
cost of aircraft creation can be achieved by improving the accuracy,
informativity, and efficiency of flight research results on free flying
dynamically similar models (FDSM). In particular, this is ensured by the
development, improvement, generalization, and application of theoretical and
methodological foundations for the creation of FDSM. This paper is structured
from these positions. It does not reveal all the peculiarities of the design,
manufacture, and testing of FDSM but shows the influence and dependence of
altitude-velocity limitations of physical modelling problems on the main
parameters of FDSM. At the same time, a literature review was performed to
study and analyze the achievements and problems of
physical modeling of aircraft flight on FDSM. The
conditions and scales of similarity used in the design, manufacture, ground and
flight tests of FDSM, and flight research are considered. The influence on the
main parameters of FDSM of modelling problems, together with similarity conditions
and the system of relations of parameters of FDSM, of the full-scale aircraft
and environment; design conditions; technological limitations; flight-technical
requirements; and operational limitations is emphasized. It is established that
if mass is taken as the objective function in the design of an FDSM, then in
order to achieve its minimum, one should strive to create an FDSM with the
minimum possible linear sizes. To take into account the auto-model limitations
of modelling problems, a special method for predicting flight characteristics
and scientific-research capabilities of an FDSM has been developed and
presented.
Keywords: altitude-velocity limitations, modelling problems, main parameters,
free flying dynamically similar aircraft models
1. INTRODUCTION
The most effective solution to many problems of
creating modern aircraft is the application of a method that uses as a flight
research tool a free flying dynamically similar aircraft model (FDSM), which is
an unmanned aerial vehicle for research purposes, reusable, capable of
remotely-piloted or automatic flight according to a given program [1].
As an example, Figure 1
shows images of a full-scale aircraft and its FDSM in AirStar NАСА program [2].
Fig. 1. Full-scale
aircraft and its FDSM in AirStar NАСА program
The process of creating an FDSM has a whole set
of features that distinguish it from a similar process for aircraft of other
purposes. The main one is the is necessity to satisfy the accepted (taking into
account the modelling tasks) similarity conditions at all stages of design,
manufacture, ground and flight tests of FDSM, as well as to conduct both
leading and accompanying flight research. To reveal the features of creating
FDSM it is necessary to answer numerous questions, which cannot be done in one
small work. However, it is feasible to show the influence and dependence of
altitude-velocity limitations of physical modelling problems on the main
parameters of FDSM.
The purpose of this work
is to reduce the time and costs of aircraft creation by increasing the
accuracy, informativity, and efficiency of flight research results on FDSM,
which is provided by the development, improvement, and application of
theoretical and methodological bases of their creation.
2. LITERATURE REVIEW ON PHYSICAL MODELLING OF
AIRCRAFT FLIGHT, THEORETICAL AND METHODOLOGICAL BASES FOR CREATING FDSM AND
CONDUCTING FLIGHT RESEARCH ON THEM
Since
1927, NАСА
carried out a set of works to create FDSM of various aircraft and conduct
flight research of flight dynamics on them. At the same time, a number of
countries have developed theoretical and methodological apparatus for the
design, manufacture, and flight testing of FDSM, as well as flight research on
them. These principles, methods and techniques are based on extensive
experimental material and have been repeatedly tested in the process of real
design and flight research. Currently, not all problems in physical modeling on FDSM have been solved: conclusions and
recommendations for known problems require analysis, improvement, and
generalization, and new problems require different approaches to their solution
[2, 4, 6].
3. SCALES OF SIMILARITY OF THE MAIN PARAMETERS
OF FDSM
The
similarity conditions in the creation of FDSM eliminate a number of design and
manufacturing problems common to aircraft for other purposes. These conditions
together with the conditions of feasibility of FDSM and flight-technical
requirements, impose on the parameters of FDSM and conditions of flight
experiments a system of relations, the correct resolution of which is one of
the most difficult theoretical problems of this type of physical modelling.
Reliable transfer of the results of research flights of FDSM to a full-scale
aircraft is possible only if the conditions of geometric, kinematic, and
dynamic similarity are met: an FDSM should have the same external shape as a
full-scale aircraft, the position of the center of
mass (CM) required by similarity and mass-inertial parameters,
elastic-geometric characteristics, and similar laws of the automatic control
system. As a result, an FDSM will behave in flight in the same way as a
full-scale aircraft under relevant conditions [1, 3, 5].
In
the analysis of similarity issues, first of all, attention is paid to the
scales of similarity, which allow us to find the relationship between the
relevant parameters and characteristics of a full-scale aircraft and an FDSM,
as well as the parameters and characteristics of the modeled
phenomena. Since for an FDSM its characteristic linear size 
,
mass 
,
axial 
, 
, 
and centrifugal 
, 
, 
moments of inertia are taken as the main
parameters, the scales of similarity between the main parameters of a
full-scale aircraft and an FDSM are as follows [5]:
; 
; 
, (1)
where 
– scale of linear size; 
– similar to ,
(m) characteristic linear size of the full-scale aircraft, (m); 
– mass scale; 
– mass of the full-scale aircraft (kg); 
– scales of moments of inertia; 
– moments of inertia (axial and centrifugal) of a
full-scale aircraft with respect to axes similar to the coordinate system of an
FDSM, (
); 
– scale of air densities; 
, 
– air density at flight altitudes 
(m) of a full-scale aircraft and 
(m) of an FDSM (
).
It
should be noted that already in formulas (1) the dependence of scales and on flight altitudes 
of a full-scale aircraft and 
of FDSM can be implicitly seen. The formulas
(1) do not give the same dependence for the scale .
Furthermore, there is no reason to claim that the flight altitudes of and are aerodynamic similarity altitudes for all
modeling problems.
The
geometrical parameters of the FDSM and, consequently, the scale are influenced by [6]:
1. Modeling problems,
together with similarity conditions and a system of relations between the
parameters of an FDSM, a full-scale aircraft, and the environment.
2. Design conditions concerning the provision of
an internal volume sufficient for the placement of on-board equipment and
component parts within the contour of the FDSM (
),
as well as ensuring the possibility of adjusting the position of the CM and
mass-inertia parameters of the FDSM (if 
).
3. Technological limitations taking into account
the capabilities of the FDSM parts manufacturing methods (for example, waviness
and roughness of the skin surface) and linkage of technological equipment (
).
4. Flight-technical requirements taking into
account the method of bringing an FDSM to the flight regime required for the
research, parameters, and characteristics of a particular carrier (
, 
).
5. Operational limitations taking into account
the need to ensure the convenience of working with an FDSM during ground tests,
preparation for test and research flights, and repair (
).
It
should be noted that the scale depends on the accepted similarity criteria
(Froude 
,
Reynolds 
and Mach 
),
which define aerodynamic similarity and include the similarity of force
interactions of airflows with streamlined bodies, and also express certain
requirements for the physical properties of the medium of the considered
full-scale and modeled flow. The influence of the similarity criteria is not
uniform in any particular case of motion, so there is practically no need for
simultaneous satisfaction (corresponding equality) of the , and criteria. However, studies have established
the mandatory criterion similarity in flight dynamics
modeling. Therefore, when modeling the flight of full-scale aircraft on FDSM,
the following combinations of similarity criteria are possible [7-9]:
1. At the same time, the similarity conditions on
, and criteria are satisfied. Under Standard
Atmosphere (SA) conditions, this is
only possible at 
and scales 
, 
, 
and 
,
which means that the external contours, masses, moments of inertia and position
CM of a full-scale aircraft and an FDSM are identical. However, FDSM can be
made of different materials, have different structural and power schemes and
on-board equipment. Such FDSM allow to research practically all flight regimes
of full-scale aircraft.
2. The similarity condition is satisfied only by
the criterion at auto-modelity according to the
criteria and .
This is the only combination of criteria in which the choice of scale does not depend on the heights of the
aerodynamic similarity and .
However, after selecting the scale and assigning the and ,
the scales and are uniquely determined by relations (1).
3. The similarity conditions according to
criteria and at auto-modelity according to the criterion .
At this combination of similarity criteria:
; 
; 
, (2)
where 
, 
– coefficients of kinematic viscosity of air
at altitudes and , (
); 
, 
– acceleration of gravity altitudes and , (
).
Using
the SA, by formulas (2) it is possible to plot graphs on dependences of , and on aerodynamic similarity heights and (Fig. 2, a), which are necessary for operative
solution of design problems of FDSM.
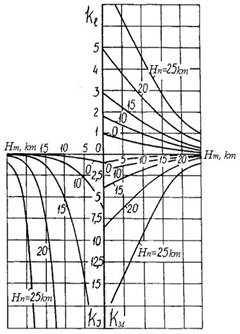
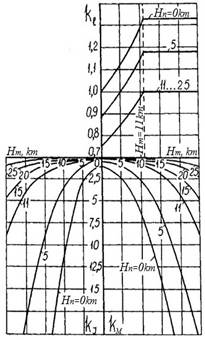
a
b
Fig.
2. Graphs of dependences , and on aerodynamic similarity altitudes and :
at satisfaction of similarity conditions according to criteria and at auto-modelity according to criterion (а) and according to criteria and at auto-modelity according to criterion (b)
As
a rule, there is more than one pair of aerodynamic similarity altitudes (, ),
for which the scales , and have acceptable values. AN FDSM with such
scales is physically feasible and capable of investigating a certain flight
regime or maneuver of a full-scale aircraft. At the same time, the flight
altitude of a full-scale aircraft (at a fixed value of scale )
corresponds to a single value of the flight altitude of an FDSM, i.e., there is
only one pair (, ).
4. The
similarity conditions according to criteria and at auto-modelity according to the criterion .
At this combination of similarity criteria:
; 
; 
, (3)
where 
, 
– temperature of incoming airflow at altitudes
and ,
(K).
Similarly
to the previous combination of similarity criteria using the SA, but using
formulas (3) it is possible to plot and use graphs of the dependencies , and on the aerodynamic similarity altitudes and (Fig. 2, b).
The
number of pairs of aerodynamic similarity altitudes (, )
is determined by the accepted scale of ,
and the range of flight altitudes of the FDSM. In this combination, as in the
previous one, the flight altitude of a full-scale aircraft (at a fixed value of
scale )
corresponds to a single value of the flight altitude value of an FDSM, i.e.,
there is only one pair (, ).
According
to the above, it follows that when pairwise combinations of similarity criteria
are satisfied, the scales , , is limited and can take the following values
[1, 5]:
а) at 
m, 
m
-
for the combination of and
; 
; 
,
-
for the combination of and
; 
; 
;
b)
at 
m, 
m
-
for the combination of and
; 
; 
,
-
for the combination of and
; 
; 
.
Experiment
altitudes have their limitations due to the capabilities of the launch system
as well as the technical capabilities of the braking and soft-landing system of
FDSM. This fact is taken into account by introducing appropriate limits on the
scale values 
,
determined by the permissible range of altitudes of the experiments.
In
the case of satisfying only the criterion (i.e., at modeling a given area of
flight regimes, and, therefore, its coverage by the area of modeling flight
regimes of a full-scale aircraft) the values are determined by the inequality [5]:
, (4)
where 
, 
– air density at minimum 
,
(m), and maximum 
(m) flight altitudes of the full-scale
aircraft specified for the research, (); 
, 
– air density at minimum 
,
(m) and maximum 
,
(m) flight altitudes of an FDSM, ().
When
criteria and or and are satisfied together (i.e., when modeling
specific flight regimes or maneuvers of full-scale aircraft), the limits of are determined by the inequality [5]:
, (5)
where 
– air density at the flight altitude of the
full-scale aircraft assigned for simulation, ().
In
case of simultaneous fulfillment of all basic airflow
similarity criteria (, and ) 
1, 
1.
In
the final determination of the limits of possible value scales (
)
and (
),
all constraints imposed on them are taken into account.
We
investigate the question of changing 
with an increase in the linear sizes of FDSM
(i.e., decreasing from 
to 
).
When
all basic airflow similarity criteria (, and ) , , , .
The values of linear sizes, mass, and moments of inertia of the FDSM in this
case are uniquely determined, and the designer has no possibility to vary them.
In
case two of the three similarity criteria ( and or and )
are satisfied, a decrease in leads to decrease in and ,
i.e., an increase in the linear sizes of the FDSM (according to relations
(1)–(3) or graphs in Fig. 2, а and 2, b) entails in increase in its required mass
and moments of inertia. It is also important that a decrease in (at 
)
leads to the need to perform modelling experiments at higher altitudes .
The cases under consideration allow for modeling within the auto-modelity zones
both a certain mode (
at ),
and specified maneuvers with velocity change (
at ).
Satisfying
only the makes it possible to modeling within the
auto-modelity zones according to the and criteria both a certain mode ( at )
and specified maneuvers with altitude or velocity changes ( at 
or at ),
as well as a limited area of flight regimes ( at )
of a full-scale aircraft. This follows from the independence of the scale from the altitudes ,
and ,
and from the fact that the same values of can be achieved for different pairs (, ).
Suppose
that there is a range of values of the scale .
Then for any of these values (according to relations (1)), a decrease in the
scale leads to a decrease in the scales and ,
i.e., to an increase in the required values of mass and moments of inertia of
the FDSM. The minimum required values of mass and moments of inertia are
achieved for the pair , 
.
If the "descent" carried out in the from to (outer cycle) and by scale from to 
(inner cycle), then the first value of the
mass satisfying the constraints will be minimum
required (the moments of inertia will also be minimum), and the scale value – maximum. Further downscaling of or ,
at best, only the same value of the required mass of an FDSM can be obtained.
Since
mass is usually taken as the objective function in the design of an FDSM, in
order to achieve its minimum, one should strive to create an FDSM with the
minimum linear sizes, since an increase in the overall sizes of an FDSM
inevitably entails an increase in its required mass [5].
4. METHOD FOR PREDICTING THE FLIGHT
CHARACTERISTICS AND RESEARCH CAPABILITIES OF FDSM OF AIRCRAFT
When
designing FDSM, equality of possible and required values of main parameters,
satisfaction of flight-technical requirements for FDSM are achieved, and then a
special method is used to predict the flight characteristics and research
capabilities of FDSM of aircraft.
Its
essence consists in the following: calculation of altitude-velocity limitations
of flight characteristics of the FDSM, construction of the model flight regime
area (MFRA) and its analysis (Figs. 3, 4); displaying of the MFRA into the area
of modelling aircraft flight regimes (AMAFR); comparison of AMAFR with flight
regimes specified for the research from the aircraft flight regime area
(AFRA); analysis of the results, and formation of a conclusion about the
capabilities of the FDSM as a research tool.
The
result of calculation and analysis of the MFRA is a conclusion about the design
altitude-velocity characteristics of an FDSM with a specific set of main
parameters, but the conclusion about its capabilities as a research tool is
made only after construction of the AMAFR.
Each
point 
of the MFRA in the coordinate system 
characterizes a certain altitude-velocity
flight regime of an FDSM, and the point 
of the AMAFR in the coordinate system 
–
a certain altitude-velocity flight regime of a full-scale aircraft, which, in
principle, can be researched on an FDSM with the considered set of main
parameters.
Any
curve in coordinates ,
limiting the MFRA, is displayed in coordinates 
by corresponding curve-limitation of the
AMAFR. The procedure of displaying the MFRA into the AMAFR consists of the
transition from the MFRA in coordinate system to the AMAFR in the coordinate system and is performed using the scale value and the SA by the formulas [5]:
(6)
where 
, 
–
air density and acceleration of gravity at the altitude 
,
(m) of a full-scale flight, ().
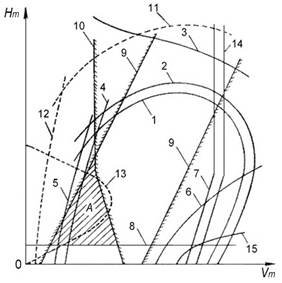
Fig. 3. System of
altitude-velocity limitations of MFRA [5]: 1 – by maximum velocity of steady
horizontal flight; 2 – by planning speed; 3 – by critical dive velocity; 4 – by
minimum velocity of steady horizontal flight; 5 – by stall velocity; 6 – by maximum
permissible velocity head; 7 – by aerodynamic heating limit temperature; 8 – by
minimum permissible flight altitude; 9 – by dynamic similarity conditions with
respect to auto-model values of Reynolds criterion ; 10 – by dynamic similarity
conditions with respect to auto-model values of Mach criterion ; 11 – by maximum carrier flight
velocity; 12 – by minimum carrier flight velocity; 13 – by maximum flight
velocity at ground launch; 14 – by engine operating conditions; 15 – by maximum
operational overload; А – example of the area of
possible researches at auto-modelity by criteria and
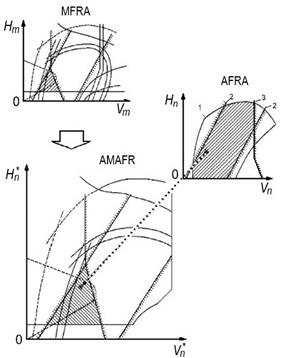
Fig. 4. Scheme for determining
the capabilities of an FDSM as a research tool [5]: 1 – limits of AFRA; 2 –
limits of auto-modelity zone on the AFRA according to
the criterion ; 3 – limits of auto-modelity
zone on the AFRA according to the criterion
Using the display procedure, the
AMAFR is determined, which is directly compared with the regimes specified for
research from the AFRA, since the scales in the coordinate systems of the AMAFR and 
of the AFRA are the same.
Based on the results of this
comparison, a conclusion is made about the possibilities of researching the
aircraft flight regimes specified in the project task on its FDSM with a
specific set of main parameters. The final selection of the main parameters of
the FDSM is carried out as a result of optimization by mass , which is both a parameter of
the FDSM and an objective function.
5. CONCLUSIONS
The work is carried out from the standpoint of analysis,
improvement, and generalization of the existing theoretical and methodical
foundations of creating FDSM. This, to a certain extent, made it possible to
fulfill the goal of the work – to reduce the time and cost of creating aircraft
by improving the accuracy, informativeness, and efficiency of flight research
results on FDSM. The paper does not consider all the features of creating FDSM
but shows the influence and dependence of altitude-velocity limitations of
physical modeling tasks on the main parameters of FDSM of aircraft.
At the same time, a literature review was conducted to
study and analyze the achievements and problems of aircraft flight physical
modeling, the theoretical and methodological foundations of creating FDSM, and
the conduct of flight studies on them. It was determined that the method of
researching aircraft flight characteristics on free flying dynamically similar
models is widely used in the practical activities of aviation institutes and
firms.
In the paper presented herein, the conditions and scales
of similarity used in creating FDSM and conducting flight studies on them are
considered. The influence on the main parameters of FDSM of modeling tasks,
together with the similarity conditions and the system of relations of
parameters of FDSM, of the full-scale aircraft and the environment; design
conditions; technological limitations; flight-technical requirements;
operational limitations is emphasized. A specific method for predicting flight
characteristics, and research capabilities of FDSM using a unique display
procedure is developed and presented.
When discussing programs performed or being carried out
in aviation institutes and firms, it should be noted that information about the
theoretical foundations of creation, design features, technology of production
of FDSM and flight studies, as well as other features of this promising method
in the open press, is limited [8-10]. And, nevertheless, it is possible to
assert with confidence that the results of theoretical studies of the authors
presented in the paper are in good agreement with the results of similar
studies of scientists dealing with the problems of modeling the dynamics of
aircraft flight in the Earth's atmosphere.
References
1.
Sadovnychiy
Sergei, Alexander Betin, Alexander Ryshenko. 2005. „Flight control system
damage simulation using freely flying models”. The Aeronautical Journal 109(1091):
45-50. DOI: 10.1017/S000192400000052X.
2.
Chambers
Joseph R. 2010. Modeling flight: The Role of Dynamically Scaled
Free-Flight Models in Support of NASA’s Aerospace Programs. Washington:
NASA. ISBN: 978-0-16-084-633-5.
3.
Cook
Michael V. 2007. Airplane Flight Dynamics principles. Oxford: Elsevier.
ISBN: 978-0-7506-6927-6.
4.
Bogos
Stefan, Ion Stroe. 2012. „Similarity criteria for “full” and “scale” aircraft
on the lateral stability analysis”. UPB Scientific Bulletin, Series D
74(4): 13-26. ISSN: 1454-2358.
5.
Sadovnychiy
Sergei, Viktor Ryabkov, Alexander Ryshenko, Javier Sandoval. „Modelling of
Aircraft Flight by means of Dynamically Similar Models with a Flight Control
Systems Similarity”. In: Modelling and simulation technologies conference:
meeting paper: 326-334. American Institute of Aeronautics
and Astronautics, New Orleans, L.A., U.S.A.
11-13 August, 1997. DOI: 10.2514/6.1997-3792.
6.
Olejnik
Aleksander, Stanisław Kachel, Robert Rogólski, Jaroslaw
Milczarczyk. 2021.
„Conception of developing the dynamically
similar downscaled medium-range passenger airplane model for in-flight testing”.
Proceedings of the Institution of Mechanical
Engineers, Part G: Journal of Aerospace Engineering 235(1): 104-116.
DOI: 10.1177/0954410020934301.
7.
Shakoori
Ali, Mahdi Mortazavi, Hadi Nobahari. 2012. „Aircraft dynamically similar model
design using simulated annealing”. Applied Mechanics and Materials 225:
323-328. ISSN: 1662-7482. DOI: 10.4028/ www.scientific.net/AMM.225.323.
8.
Pusztai Daniel, Mark H. Lowenberg,
Simon A. Neild. 2024. „Flight Testing of a Dynamically Scaled Transport Aircraft
Model for High-Alpha Wind Tunnel Data Validation”. In: AIAA SCITECH 2024 Forum: meeting paper:
1497. American Institute of Aeronautics and Astronautics, Orlando, FL, U.S.A. 8-12 January, 2024. DOI: 10.2514/6.2024-1497.
9.
Akaryildiz Bora, Resit
Demirkiran, Omer Ozyilmaz, Muhammed Emin Tals. 2024. „Scale Factor Oriented Control Parameters
Tuning Procedure for Dynamically Scaled”.
In: AIAA SCITECH 2024 Forum: meeting paper:
2876. American Institute of Aeronautics and Astronautics, Orlando, FL, U.S.A. 8-12 January, 2024. DOI: 10.2514/6.2024-2876.
10.
Nguyen Nhan T., Benjamin Webb. 2025. „Analytical Flight Dynamic Model
Development for eVTOL Aircraft Aircraft”.
In: AIAA SCITECH 2025 Forum: meeting paper:
0657. American Institute of Aeronautics and Astronautics, Orlando, FL, U.S.A. 6-10 January, 2025. DOI: 10.2514/6.2025-0657.
Received 04.05.2025; accepted in revised form 19.07.2025
Scientific Journal of Silesian
University of Technology. Series Transport is licensed under a Creative
Commons Attribution 4.0 International License