Article citation information:
Popiela, K., Wasiak, M. A A method of loading
unit formation taking into account mass, load-bearing strength and surfaces of
packing units. Scientific Journal of
Silesian University of Technology. Series Transport. 2017, 96, 151-160. ISSN: 0209-3324. DOI: https://doi.org/10.20858/sjsutst.2017.96.14.
Kamil POPIELA[1], Mariusz
WASIAK[2]
A METHOD OF LOADING UNIT
FORMATION TAKING INTO ACCOUNT MASS, LOAD-BEARING STRENGTH AND SURFACES
OF PACKING UNITS
Summary. The
problem of loading unit formation is computationally complex in nature. This
article presents a heuristic algorithm of forming unit loads, which can be
applied to unit load arrangement on unit load devices. This method accounts for
dimensional, mass and load-bearing strength of loading units and loading
devices. Moreover, the rotation of packages about a 90° vertical axis has been
made possible. In this algorithm, the bearing surface of each packing unit is
entirely supported. This guarantees the stability of additional unit load
layers. A sample calculation of the arrangement of 30-unit loads is presented
in this article.
Keywords:
forming loading units; heuristic algorithm of loading unit formation;
load-bearing strength of packing units
1.
INTRODUCTION
The arrangement of loading units is
one of the more challenging problems to solve in the field of transport due to
its computational complexity. For problems with medium to large quantities of
loading units, it becomes impossible to obtain solutions that better utilize the
use of loading space and, at the same time, guarantee cargo safety. To date,
the optimization problem models and heuristic methods, which have been
developed, have not been able to correctly obtain solutions for all decision
alternatives. By and large, the results obtained have erroneous physical
interpretations. Moreover, the existing models do not account for packing
unit-bearing surface support, mass and the load-bearing strength of both
packing units and unit load devices.
The optimization problem models,
which do result in accurate physical interpretations [11, 12, 21], are characterized by long
solving times for problems with small quantities of packing units. For this
reason, existing models cannot always be applied to logistics systems as
support systems.
The commonly used empirical
approach, which requires a shorter execution time to obtain unit load formation
solutions, offers significant advantages over complex optimization methods or
even heuristic methods in filling loading devices. Utilizing this approach,
however, results in an increased risk of damaging unit loads due to the
excessive weight of stacked packing units.
Taking all of the above into account,
studies were undertaken to develop a new heuristic method of forming unit
loads. The obtained results are presented and described in this article.
2. LITERATURE REVIEW
Heuristic methods, by nature,
contain simplifying assumptions. In the case of unit load formation problems,
they can be divided into three methods: guaranteeing or failing to guarantee
packing unit-bearing surface support, considering or failing to consider the
rotation of packing units, and taking into account or failing to take into
account the load-bearing strength and durability of packing units.
Heuristic methods, in which rotation
of packing units is possible about an axis, have been proposed by Gehring and
Bortfeldt [9], Wang, Li and Levy [19], Wu, Li, Goh and de Souza [20], and Engeblad and Pisinger [8].
Engeblad and Pisinger [8] developed an iterative heuristic
method for a two-dimensional packing problem based on a method of two
permutations containing packing unit numbers described in [14].
Additionally, building on an original algorithm in [8], a heuristic method for a
three-dimensional packing problem was proposed, where the packing units
arranged in a loading device represent three permutations respective to each dimension.
This algorithm did not account for load-bearing strength, durability and mass
of packing units. Complete support for bearing surfaces of packing units was
also not included in this method.
Another approach to solving this
problem was presented by Wu, Li, Goh and de Souza [20]. The authors applied two genetic
algorithms in order to solve a three-dimensional packing problem for cuboid
packing units. With the help of the first algorithm, it is possible to obtain a
solution for a single-unit load formation. The second algorithm allows for many
unit loads to be formed from various sized packing units and loading devices.
These algorithms can be used to form unit loads by solely considering the size
of packing units. The remaining parameters, for example, mass and the
load-bearing strength and durability of packing units, are not taken into
account. Moreover, the complete support of bearing surfaces is not ensured,
which fails to guarantee the stability of the formed loading units.
A solution for arranging pallets in
a container was proposed by Sheng, Hongxia, Xisong and Changjian [18]. In an effort to better utilize
loading space in a container, where additional unit loads cannot fit, the
arrangement of packing units was taken into account.
A heuristic method composed of two
algorithms, the binary search tree and the greedy algorithm, was developed.
First, the binary search tree arranges unit loads in a container. Next, using
the greedy algorithm, packing units, which did not fit, are positioned in the
remaining free space. In this heuristic method, it is possible to rotate
packing units and loading units about three axes. Moreover, the arranged
packing units and unit loads have adequate support for their bearing surfaces.
Aside from packing unit rotation,
the stability of the arranged load is also necessary in order to obtain
practical solutions of the unit load formation problem. Methods that take this
into consideration were proposed by Gehring and Bortfeld [9], Bischoff and Ratcliff [3,4], and Bischoff, Janetz and Ratcliff
[2]. An extension of this class of
model is presented in [16], where the maximum number of
layers that a selected packing unit may withstand was defined. This, however,
may solely be applied with respect to homogenous packing units. Arranging
additional layers of packages in a loading space requires knowledge of both
mass and load-bearing strength of the packing units.
Despite the importance of heuristic
methods available in literature, which contain constraints preventing damage to
packing units, due to their load-bearing strength, ensuring proper bearing
surface support for packing units has been neglected. In these methods, each
packing unit is characterized by a centre of mass and load-bearing strength,
depending on its placement.
An example of a method that
addresses the load-bearing sides of packing units can be found in [2]. It was proposed that packing
units should be arranged into a package subset by layer, beginning with the
load-bearing surface of the loading device. The following layers should be
added until the loading space becomes maximally filled. Each package subset is
made up of one type of packing unit, which is arranged length- and widthwise
without stacking. This model proposed arranging a maximum of two package subset
types in each layer. The authors suggested this in an attempt to tackle the
problem of varying heights in each individual layer.
In the heuristic method, accounting
for the load-bearing strength of packing units is less complicated if the units
have identical mass and strength characteristics. In this case, placing
packages directly on top of another does not require calculating the sum of
individual masses, dependent on the bearing support surface of packing units.
Methods that reflect this concept have been introduced by Liu, Lin and Yu [13], and Gendreau, Iori, Laporte
and Martello [10].
In contrast to the method described
in [13], Bischoff [1] acknowledged the fact that packing
units not only vary in shape and size, but also in load-bearing strength. In
this method, complete load-bearing surface support of packing units was taken
into consideration. The available loading space is recorded in two matrices.
The first matrix contains data pertaining to the height of the available
loading space and the second contains the load-bearing strengths.
A similar approach to the method
described in [1] was presented by Gehring and
Bortfeldt [9]. Five constraints were utilized in
the genetic algorithm for forming container unit loads developed by the
authors. The first constraint allowed for the ability to rotate packing units.
A portion of the packing units can be rotated about three axes; however, the
remaining packing units can only be rotated about a horizontal axis. The next
two constraints enabled a package to be placed in a column, due to the
load-bearing strength of the supporting packages. These columns do not transfer
their vertical weight and are formed from heterogeneous packing units in a way
that maximizes the use of container space. The next constraint in the algorithm
is responsible for load stability, which is dependent on the support of bearing
surfaces and the determination of the centre of mass for container loading
units. It is assumed that the centre of mass of packing units is located at
their geometric centre. Thus, the packing units are stable, as long as the
entire load-bearing surface is directly supported by another packing unit.
The suggested approach in [1] seems to be simplified due to the
fact that the possibility to directly support packing unit surfaces with
multiple packing units is omitted. Additionally, the assumption that the
packing unit’s mass is located at the geometric centre and its resulting
transfer of force is independent of the supporting surface. As a result of this
simplification, the weight of each loading unit is transferred through the
loading unit that supports the geometric centre of its base. Therefore, it is
justified to claim that this model should be further developed in order to
include the vertical weight transfer under the condition that the mass of each
packing unit should be distributed throughout the entire surface of its base.
Similarly to the approach described
in [1] and [9], Ratcliff and Bischoff [17] presented their method, which
included an algorithm presented in [2]. In their approach, they
considered the vertical weight transferred through packing units, dependent on
the bearing surface support of the remaining packing units. Despite the fact
that this method takes into account the load-bearing strength of each packing
unit, the vertical load-bearing strength is only identified for individual
layers of packages. This ensures the safety of packing units; however, it is
obtained at the expense of efficiently utilizing loading space. In order to
improve the quality of solutions, it is necessary to make the load-bearing
strength of packing units independent of the average strength of cargo layers.
Most of the heuristic methods found
in the literature [5, 6, 7, 14] make it possible to obtain a
solution that maximally fills a loading space. By and large, in heuristic
methods, the ability to transfer weight through packing units is neglected. In
the methods where this is considered, the bearing surface support of packing
units or the ineffective use of loading space is overlooked more than once.
In this way, the need to formulate a
heuristic algorithm for forming unit loads, in which the maximum load-bearing
weight of each packing unit is considered, as well as the acceptable level up
to which formed unit loads will be filled, is justified.
3. APPROACH TO THE
PROBLEM
The formulated algorithm is a proprietary method of
arranging packing units (PUs) in/on loading devices (LDs). This method is free
from limitations described in the literature of heuristic algorithms, which
fail to simultaneously consider the possibility of rotating PU, by transferring
vertical weight through PUs and LDs, as well as adequately supporting the
load-bearing surfaces of PUs. A flowchart of the algorithm developed for a formulated
model is presented in Fig. 1.
For the purpose of designing a heuristic algorithm, a
formalism was introduced, which includes:
- a set of
numbered PUs is PO = {1, …, i, …, n}, where n is the quantity of PUs and i
is a PU number
-
a
set of numbered LDs is UL = {1, …, j, …, m}, where m is the quantity of LDs and j
is the number of LDs
-
a
set of numbered PU sorting methods is MS = {1, …, ζ, …, σ}, where
σ is the quantity of PU sorting
methods and ζ is the method
number
-
a set of numbered PUs placed in the j-th LD for
the ζ-th PU sorting method in the form SUPO(ζ,
j) = {i: i
∈ PO, ![]() }, ζ
Î MS,
j ∈ UL, where
}, ζ
Î MS,
j ∈ UL, where ![]() = 1,
when the ζ-th sorting method of the i-th PU is arranged on
the j-th LD; in the opposite case,
= 1,
when the ζ-th sorting method of the i-th PU is arranged on
the j-th LD; in the opposite case, ![]() = 0, where i
≡ ηγ Î VPU
= 0, where i
≡ ηγ Î VPU
-
a
set of numbered PUs not arranged on any LD for the ζ-th PU sorting
method SUNPO(ζ) = {i: i ∈ PO, ![]() }, ζ
Î MS
}, ζ
Î MS
-
a
vector of numbered PUs is VPUs = [η1,
…,ηγ, …, ηδ], where δ
is the quantity of PUs and vector components VPUs, γ is the numbered vector component VPU, and ηγ
is a numbered PU such that i ≡ ηγ,
i Î PO,
-
a
vector of numbered LDs is VLDs = [λ1,
…, λj, …, λm], where m is
the number of LDs and vector components VLDs, and j is the
numbered vector component VLD,
such that j ≡ λj, j Î UL
-
the
binary variable τζi = 1, when, at the ζ-th
sorting method, the i-th PU is rotated 90° about a vertical axis; in the
opposite case, τζi = 0, i Î PO, ζ Î MS
In the first step of the algorithm (Fig. 1) the
decisive situation of forming loading units is determined and the PU characteristics
are introduced. The types of significant constraints can be selected here,
including whether or not the transfer of vertical weight is to be considered.
The required PU characteristics are adequate for the selected decision. Only a
selected variant of the algorithm is shown in Fig. 1.
In the second step, the method of forming unit loads
is selected, depending on the result of the decision. In the algorithm, there
are two different models of arranging PUs in/on LDs, which are selected
depending on the decision that is made. The first model takes into account the
load-bearing strength and mass (Fig. 1), while these parameters are omitted in
the second.
Next, according to the selected criterion, the PO
set is sorted. There are six methods of sorting PUs in the MS set, which includes
increasing and decreasing sorting according to mass, size and load-bearing
surface characteristics.
Following this, individual elements of the PO set
are assigned to a vector component VPU in such a way that ηγ
= i, i ∈ PO. Then, starting with the
first (ηγ = 1) vector
component VPU, the possibility of placing its corresponding PU on the λj
= 1-th LD (VLD vector component) is checked. When
placing a PU on the λj-th LD, it is added to the SUPO(ζ,
j) set. If the LD lacks space regarding the desired characteristics, a
potential placement in the next λj+1 LD is
checked. However, if the PU cannot be placed into any of the LDs, it is added
to the SUNPO(ζ) set. The possibility of placing the
remaining PU in the ζ-th sorting method is examined. Each following
ζ-th sorting methods of PU arrangement on/in LDs is repeated and
the VPU vector is redefined. When the sorting method ζ
≥ σ, the algorithm stops arranging PUs and selects the best
solution for formed loading units based on the given evaluation criteria.

![]()
Fig. 1. Outline of a heuristic
algorithm for forming loading units while taking into account load-bearing
strength and mass
4.
COMPUTATIONAL RESULTS
The heuristic method for forming unit loads described
in this article was implemented in the Python programming language. Next, many
sample calculations were defined and solved in order to assess the method’s
effectiveness and to verify accuracy. The obtained results were referred to
analytical solutions of the problem.
This article describes one of these examples. A
problem of arranging 30 packing units on Euro-pallets (1,200 mm x 800 mm x 144
mm in size) was solved. The maximum height of each pallet unit load was set to
1,344 mm, while the maximum load could not exceed 1,000 kg. The parameters of
packing units arranged on the pallet are listed in Table 1.
Tab.
1
Packing unit characteristics
|
PU number |
Length of PU [mm] |
Width of PU [mm] |
Height of PU [mm] |
Mass of PU [kg] |
Maximum load-bearing strength of
PU [kg] |
|
1 |
308 |
193 |
191 |
9 |
80 |
|
2 |
142 |
366 |
272 |
11 |
74 |
|
3 |
266 |
172 |
364 |
27 |
82 |
|
4 |
420 |
185 |
487 |
19 |
46 |
|
5 |
221 |
505 |
158 |
2 |
84 |
|
6 |
386 |
156 |
224 |
17 |
31 |
|
7 |
537 |
588 |
350 |
27 |
53 |
|
8 |
505 |
194 |
172 |
27 |
20 |
|
9 |
397 |
305 |
218 |
8 |
27 |
|
10 |
500 |
300 |
292 |
26 |
81 |
|
11 |
545 |
503 |
327 |
12 |
97 |
|
12 |
536 |
134 |
480 |
10 |
28 |
|
13 |
526 |
202 |
140 |
15 |
90 |
|
14 |
286 |
312 |
171 |
24 |
66 |
|
15 |
355 |
304 |
343 |
4 |
54 |
|
16 |
492 |
212 |
339 |
29 |
15 |
|
17 |
258 |
162 |
233 |
9 |
10 |
|
18 |
413 |
126 |
318 |
4 |
15 |
|
19 |
394 |
583 |
279 |
6 |
10 |
|
20 |
145 |
451 |
175 |
26 |
30 |
|
21 |
348 |
388 |
230 |
6 |
10 |
|
22 |
377 |
104 |
103 |
24 |
51 |
|
23 |
369 |
333 |
315 |
25 |
50 |
|
24 |
300 |
329 |
300 |
18 |
54 |
|
25 |
100 |
100 |
486 |
5 |
80 |
|
26 |
393 |
122 |
234 |
18 |
78 |
|
27 |
184 |
201 |
165 |
9 |
80 |
|
28 |
382 |
128 |
332 |
16 |
52 |
|
29 |
161 |
408 |
104 |
23 |
51 |
|
30 |
230 |
448 |
217 |
13 |
30 |
As a result of solving a sample
problem using the heuristic method, an arrangement of packing units on two
pallets was obtained. Packing units numbered 1-9 and 11-15 were placed on the
first pallet, as illustrated in Fig. 2. On the second pallet, shown in Fig. 3,
packing units numbered 10 and 16-30 were arranged. The solving time for this
problem was 2 s. In the solution, the conditions of bearing surface support
while stacking and the possibility of rotation were also met.
On the basis of the obtained
results, the proposed heuristic algorithm of forming loading units was found to
be valid. In addition to yielding a realistic solution (a logical physical
interpretation), it is possible to create an accurate visual representation of
pallet loading units.
However, after analysing the
solutions to various problems, it has been concluded that additional
improvements should be made to the packaging unit sorting algorithm, as well as
other elements of the algorithm in order to better utilize the loading space.
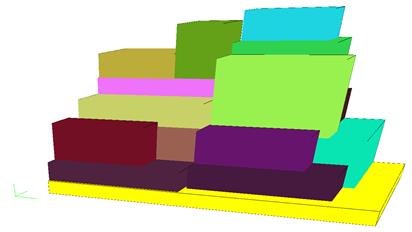
Fig. 2. The first pallet loading
unit
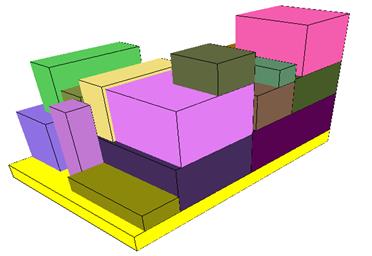
Fig. 3. The first pallet loading
unit
5.
CONCLUSION
With the help of a formulated
implementation of the heuristic algorithm, it is possible to form unit loads in
which the packaging units may be heterogeneous with regard to size, mass and
load-bearing strength. In this method, the support of load-bearing surfaces and
vertical weight transfer, dependent on bearing surfaces, was ensured.
Additionally, the limitations of loading device load-bearing strength and
vertical weight transfer, as well as the possibility to rotate packing units by
90° about a vertical axis, were taken into account.
This tool can effectively form
loading units for sample problems of up to 1,000 packing units. Moreover, with
the help of the computer implementation of this heuristic algorithm, it is
possible to solve sample problems for selected decisions, whose solutions may
be applied in the logistics industry.
Due to the advantages of using a
heuristic method to obtain solutions for a large amount of packing units in a
short resolution time, additional changes can be made to the packing unit
sorting method, while the possibility of supporting the load-bearing surfaces
of packing units with multiple packing units can be introduced to further
improve results. These changes should considerably improve the degree of
loading space utilization and make it applicable to solving a wide range of
complex packing unit arrangement problems.
References
1.
Bischoff Eberhard.E. 2006. “Three-dimensional packing of items with
limited loading bearing strength.” European
Journal of Operational Research 168(3): 952-966. ISSN 0377-2217.
2.
Bischoff Eberhard E., F. Janetz, M.S.W. Ratcliff. 1995. “Loading pallets with non-identical items.” European Journal of Operational Research 84(3):
681-692. ISSN 0377-2217.
3.
Bischoff
Eberhard E., M.S.W. Ratcliff. 1995. “Issues in the development of approaches to
container loading.” Omega 23(4):
377-390. ISSN 0305-0483.
4.
Bischoff E.E., M.S.W. Ratcliff. 1995. “Loading multiple pallets.” Journal of the Operational Research Society 46(11): 1322-1336. ISSN 0160-5682.
5.
Bortfeldt Andreas, Hermann Gehring. 1998. “Applying Tabu search to container loading problems.” Operations Research Proceedings vol.
1997: 533-538. Berlin,
Heidelberg: Springer. ISBN 978-3-540-64240-4.
6.
Chien Chen-Fu, Lee Chian-Yen, Huang Yi-Chao, Wu
Wen-Ting. 2009. “An efficient
computational procedure for determining the container loading pattern.” Computers & Industrial Engineering 56:
965-978. ISSN 0360-8352.
7.
Chua Chee Kai, V.
Narayanan, J. Loh. 1998. “Constraint-based
spatial representation technique for the container.” Integrated Manufacturing Systems 9(1): 23-33. ISSN 0957-6061.
11.
Junqueira,
Leonardo, Reinaldo Morabito, Denise Sato Yamashita. 2010. “Modelos de
otimização para problemas de carregamento de contêineres com
considerações de estabilidade e de empilhamento.” [In English:
“Optimization models for container loading problems with stability and stacking
considerations”.] Pesquisa Operacional 30(1): 73-98. ISSN 0101-7438.
14.
Martello Silvano,
David Pisinger, Daniele Vigo. 2000. “The three-dimensional bin packing
problem.” Operations Research 48:
256-267. ISSN 0030-364X.
15.
Murata Hiroshi,
Kunihiro Fujiyoshi, Shigetoshi Nakatake, Yoji Ka`jitani. 1996.
“VLSI module placement vased on rectangle-packing by the sequence-pair.” IEEE Transactions on Computer-aided Design
of Integrated Circuits and Systems 15(12): 1518-1524. ISSN 0278-0070.
17.
Ratcliff M.S.W.,
Eberhard E.Bischoff. 1998. “Allowing for weight considerations in container
loading.” OR Spektrum 20: 65-71. ISSN 0171-6468.
21.
Karrapan Claudia, Mndeni Sishange, Elana Swanepoel, Peter J. Kilbourn.
2017. “Benchmarking criteria for
evaluating third-party logistics providers in South Africa.” Journal of
Transport and Supply Chain Management 11: 1-10. DOI: http://doi.org/10.4102/jtscm.v11i0.305. ISSN 2310-8789.
Received 11.04.2017; accepted in revised form 30.07.2017
![]()
Scientific Journal of Silesian
University of Technology. Series Transport is licensed under a Creative
Commons Attribution 4.0 International License